Todos los cuerpos se encuentran formados por partículas que poseen carga eléctrica, el hecho de que no percibamos habitualmente interacciones eléctricas, y sí gravitatorias, siempre nos podemos caer, es debido a que en el caso de las masas todas se atraen, y en el caso de las cargas hay de dos tipos, todos tenemos el mismo número de cargas de ambos tipos por lo que sus efectos normalmente se anulan.

Podemos hacer experiencias en las que se muestra también que las interacciones entre las cargas vienen dadas por una expresión totalmente similar. La carga eléctrica es una propiedad de las partículas elementales que forman la materia que conocemos, que son los electrones y los quarks. Aunque las fuerzas eléctricas son comparativamente más fuertes que las gravitatorias, no podemos tomar una cantidad de carga y enfrentarla a otra con la facilidad con la que tomamos un kilogramo de hierro y lo enfrentamos a otro kilogramo. Coulomb (1736 - 1806) consiguió realizar esta experiencia utilizando una balanza similar a la de Cavendish

Si frotamos diferentes objetos podemos observar algunos efectos de interacción electrostática, se desprende de este hecho que las cargas tienen afinidades diferentes en diferentes materiales. En 1931 se le ocurrió al físico norteamericano Robert Van de Graaff construir una máquina en la que se optimizaba este fenómeno de electrificación por rozamiento.

       

Esta máquina se basa en una propiedad de los conductores, que no justificaremos, por la que si una carga se encuentra en el interior de un conductor esta se mueve a su superficie. Mediante esta máquina podemos conseguir una cantidad de carga razonable para realizar experiencias.

Vídeo cómo funciona el generador de Van de Graaff:
http://www.youtube.com/watch?v=I2G0IdTWGQU

La interacción entre cargas nos lleva a una expresión similar a la interacción gravitatoria, la fuerza varía inversamente proporcional al cuadrado de la distancia entre las cargas.

Las expresiones para la interacción gravitatoria entre dos masas puntuales y la electrostática entre dos cargas puntuales son formalmente idénticas por lo que las propiedades básicas derivadas de las expresiones matemáticas también serán iguales, en ambos casos la fuerza disminuye con el cuadrado de la distancia y la fuerza tiene la dirección de la recta que une las partículas. El sentido de estas fuerzas difiere, en el caso de las masas estas siempre se atraen, en el caso de las cargas eléctricas nos encontramos con la necesidad de distinguir dos tipos de cargas al observar que las cargas que pertenecen a un grupo se repelen pero si son de distinto grupo se atraen.

Donde a q₁ y q₂ las llamamos cargas eléctricas, la carga eléctrica es una propiedad de las partículas elementales que forman la materia, que son los electrones y los quarks, en unidades internacionales se mide en culombios, un culombio es la carga que situada a un metro de distancia de otra igual interacciona con una fuerza de un newton, esta expresión es conocida como la ley de Coulomb en honor a su descubridor.

Simulación: http://webs.um.es/jmz/IntroFisiCompu/ejs/Ejemplos/drawables/fuerza_electrostatica.html

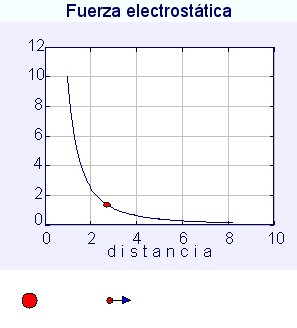
En la imagen se observa la representación gráfica de la fuerza que ejerce una carga sobre otra que podemos desplazar.

¿Qué hace que en la naturaleza, y en la tecnología, las interacciones gravitatorias y las eléctricas intervengan de modo tan diferente? Tres son los principales factores que las diferencian:

• Las cargas eléctricas pueden ser de dos tipos que denominamos como positivas y negativas, las del mismo signo se repelen mientras que de signos opuestos se atraen y en el universo existe la misma cantidad de carga de signo positivo como negativo, un cuerpo en general es neutro por lo que no apreciamos interacciones eléctricas entre ellos, mientras que todas las masas se atraen.
• Otra diferencia se encuentra en la intensidad de las fuerzas, mucho mayor para las eléctricas para las mismas escalas.
• Por último, si estudiamos situaciones en que se produzcan variaciones temporales los comportamientos gravitatorios y eléctricos dejan de tener similitudes. Si se observan las cargas en movimiento aparece una nueva interacción, la magnética, mientras que la interacción entre las masas no varía, que nosotros sepamos apreciar, si estas se mueven. El hecho de tener en cuenta variaciones temporales en los campos eléctricos y magnéticos nos abre un mundo nuevo que nos llevará al electromagnetismo, a la luz.

Las fuerzas electrostáticas, comparadas con las gravitatorias son cuantitativamente menores, en las tareas II.1, II.2 y II.3 se pueden ver ejemplos en los que se puede apreciar qué entendemos por “cuantitativamente menores”. A pesar de estas consideraciones sobre la intensidad de las fuerzas gravitatorias y eléctricas, en nuestro entorno en general prevalecen las interacciones gravitatorias frente a las eléctricas porque los cuerpos que nos rodean tienen el mismo número de cargas positivas como negativas y sus efectos se compensan mientras que las interacciones gravitatorias siempre se suman y su acción gobierna el movimiento del Sistema Solar, de nuestra Galaxia y del Universo.

Otro aspecto relevante es el comportamiento dinámico de las partículas elementales, estas partículas, que constituyen los átomos de los objetos que nos rodean y también nosotros mismos ¿se comportan como nuestro sistema solar? ¿podemos tratarlas con la mecánica newtoniana? Pensemos en dos moléculas de oxígeno de nuestra atmósfera, colisionan entre sí y con otras moléculas ¿se comportan las partículas que las forman como dos sistemas solares que colisionasen? Las estructuras atómicas que constituyen las moléculas son mucho más estables que los sistemas planetarios, su comportamiento ya no viene descrito por las leyes de Newton sino por la Mecánica Cuántica. El conocimiento del comportamiento de los electrones en estructuras sólidas compuestas por muchos átomos nos ha llevado a la utilización de conductores eléctricos hasta los chips de los ordenadores, teléfonos móviles… pasando por el transistor.