Germán Ros Sánchez
La palabra “fractal” proviene del latín fractus, que significa “fragmentado”, “fracturado”, o simplemente “roto” o “quebrado”, muy apropiado para objetos cuya dimensión es fraccionaria. El término fue acuñado por Benoît Mandelbrot en 1977 aparecido en su libro The Fractal Geometry of Nature. Al estudio de los objetos fractales se le conoce, generalmente, como geometría fractal.
Un fractal es un conjunto matemático que puede gozar de autosimilitud a cualquier escala, su dimensión no es entera o si es entera no es un entero normal. El hecho que goce de autosimilitud significa que el objeto fractal no depende del observador para ser en sí, es decir, si tomamos algunos tipos de fractales podemos comprobar que al hacer un aumento doble el dibujo es exactamente igual al inicial, si hacemos un aumento 1000 comprobaremos la misma característica, así pues si hacemos un aumento n, el dibujo resulta igual luego las partes se parecen al todo.
Un conjunto u objeto es considerado fractal cuando su tamaño se hace arbitrariamente mayor a medida que la escala del instrumento de medida disminuye.
Hay muchos objetos ordinarios que, debido a su estructura o comportamiento, son considerados fractales naturales, aunque no los reconozcamos. Las nubes, las montañas, las costas, los árboles y los ríos son fractales naturales aunque finitos ergo no ideales; no así como los fractales matemáticos que gozan de infinidad y son ideales.
Algunas definiciones sencillas extraídas de ensayos y libros acerca del tema:
Modelos infinitos comprimidos de alguna manera en un espacio finito
Bellísimos y fascinantes diseños de estructura y complejidad infinita.
Resumen de las propiedades de los fractales:
Dimensión
no entera.
Como se mostrará
en el apartado siguiente la dimensión de un fractal no es un número
entero sino un número generalmente irracional.
Compleja
estructura a cualquier escala.
Los
fractales muestran estructuras muy complejas independientemente de
la escala a la cual lo observemos.
Infinitud.
Se
consideran infinitos ya que a medida que aumentamos la precisión
del instrumento de medición observamos que el fractal aumenta en
longitud o perímetro.
Autosimilitud en
algunos casos.
Existen
fractales plenamente autosimilares de manera que el todo está
formado por pequeños fragmentos parecidos al todo.
La geometría tradicional o euclidiana distingue las siguientes dimensiones: -1, 0, 1, 2, 3.
Dimensión -1:
Realmente esta dimensión representa el vacío.
Dimensión 0: Un punto no tiene dimensión alguna porque no tiene longitud, anchura o profundidad.
Dimensión 1: Una línea (formada por infinitos puntos) es unidimensional ya que sólo tiene longitud. Si dividimos por la mitad la medida de la longitud de un objeto unidimensional, obtenemos dos objetos pequeños de idéntica apariencia al objeto original
![]()
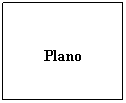
Dimensión 2: Un plano
es bidimensional porque tiene longitud y anchura. Si lo dividimos por
su longitud y su anchura obtenemos 4 planos.

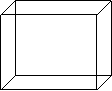
Dimensión 3: Un cubo es tridimensional ya que tiene longitud, anchura y profundidad. Si dividimos exactamente por la longitud, la anchura y la profundidad obtenemos 8 cubos más pequeños.
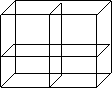
De estas observaciones se
puede concluir que la duplicación ocurre a razón exponencial de 2,
4, 8 y así sucesivamente. Aritméticamente, estos números pueden
expresarse como:
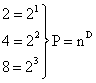
Siendo P
las porciones obtenidas del número de divisiones n
elevado a la dimensión D.
Si
examinamos el valor del exponente en cada caso, encontramos que éste
es idéntico al valor de la dimensión de cada objeto: 1, 2 y 3. Así
pues esta forma de calcular la dimensión de un objeto resulta
totalmente válida.
¿Pero qué pasa cuando
medimos la dimensión de un fractal?
Tomando de ejemplo el
triángulo de Sierpinski . Este fractal se forma descomponiendo un
triángulo equilátero en 3 triángulos iguales como vemos abajo.
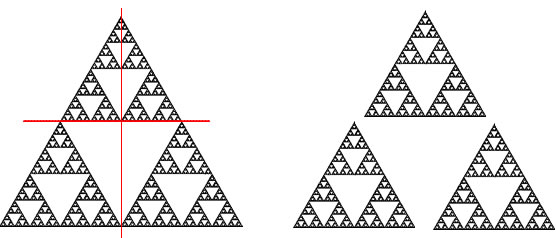
![]()
Por tanto, podemos comprobar
que este fractal tiene dimensión 1.58496.
Queda así
especificado el concepto de dimensión fractal.
Normalmente un fractal se
construye mediante una fórmula o función que se va iterando un
número arbitrario de veces. Aunque otra forma de lograrlo es
mediante la aplicación de técnicas de recursividad. Con estos dos
métodos es como solemos conseguir la autosimilitud de los fractales,
ya que aplicamos la misma función a diferentes niveles..
Tan
importante es la elección de la formula como la elección del método
de coloreado de los resultados. En relación a esto, existen multitud
de técnicas de coloreado como pueden ser:
Coloreado mediante el algoritmo de tiempo de escape.
Coloreado por convergencia a soluciones de una ecuación.
Cualquier otro que puedas imaginar.
Existen multitud de fractales
naturales en las cosas más insignificantes, y que pasamos por alto
cada día. Estos fractales no son infinitos (porque fuera del
elegante universo de las matemáticas ese concepto es difícil), pero
si son autosimilares a muchos niveles.
Claros ejemplos de estos
fractales son:
|
Ejemplos |
||
|
|
|
|
|
Hoja |
Corales |
Romanesco |
Por nuestra parte, en esta
simulación vamos a dedicar nuestra atención a fractales creados o
descubiertos por el hombre mediante ecuaciones
conocidas.
Concretamente mostraremos un especial interés en el
fractal de Newton y en cómo se construye.
El fractal
de Newton es una curiosa creación basado en la aplicación del
método de Newton para la resolución de sistemas de ecuaciones no
lineales. El algoritmo es eficiente para encontrar aproximaciones de
los ceros o raíces de una función real. También puede ser usado
para encontrar el máximo o mínimo de una función, encontrando los
ceros de su primera derivada.
La idea de este método es la
siguiente: se comienza con un valor razonablemente cercano al cero
(denominado punto de arranque), entonces se reemplaza la función que
estamos tratando por la recta tangente en ese valor, se iguala a cero
y se despeja (fácilmente, por ser una ecuación lineal). Este cero
será, generalmente, una aproximación mejor a la raíz de la
función. Luego, se aplican tantas iteraciones como se deseen hasta
que el método de una solución adecuada. Cabe destacar que es
posible que el método diverja en determinadas circunstancias que
pueden depender de la elección del punto inicial.
Además es
responsabilidad nuestra la elección de un buen test de parada,
aunque dicho test podría basarse simplemente en el número de
iteraciones realizadas (como es nuestro caso para los ejemplos).
Partiendo de este método, y dado que es capaz de aproximarse tanto a soluciones reales como a complejas, podríamos ingeniárnoslas para que dada una función se coloreasen de forma distinta las soluciones a las que el algoritmo va convergiendo. En pocas palabras: seleccionamos una región del plano complejo y vamos ejecutando el método de Newton, para una función F dada, en un punto elegido de la región.Dependiendo de a qué solución converga el método pintamos ese punto de un color u otro.
¡ Esta es la manera en la que se han pintado los fractales de Newton de las distintas simulaciones !
Como podemos comprobar, en este
caso, han surgido fractales a partir de un método de aproximación
de raíces de funciones y un poco de imaginación.
Para los
ejemplos que se verán en las simulaciones se han dibujado los
fractales basados en las siguientes funciones:
 |  |
| Fractal de Newton para la función x^3-1 | Fractal de Newton para la función x^5-1 |
El conjunto de Mandelbrot es el más
conocido de los conjuntos fractales, y el más estudiado.
Este
conjunto se define así, en el plano complejo:
Sea c un número
complejo cualquiera. A partir de c, se construye una sucesión por
inducción:
z0 = 0 (término inicial)
zn+1 = zn2 + c (relación de inducción)
 |
| Fractal de Mandelbrot |
Si esta sucesión queda acotada, entonces se dice que c pertenece al conjunto de Mandelbrot (quien es el inventor de dicho fractal), y si no, queda excluido del mismo. En la imagen anterior, los puntos negros pertenecen al conjunto y los de color no. Los colores dan una indicación de la velocidad con la que diverge (tiende al infinito, en módulo) la sucesión: en rojo oscuro, al cabo de pocos cálculos se sabe que el punto no está en el conjunto mientras que en blanco, se ha tardado mucho más en comprobarlo. Como no se puede calcular un sinfín de valores, es preciso poner un límite, y decidir que si los p primeros términos de la sucesión están acotados entonces el punto merece el honor de pertenecer al conjunto. Al aumentar el valor de p se mejora la precisión de la imagen.
Por otra parte, se sabe que los puntos cuya distancia al origen es superior a 2 : x2 + y2 > 4 no pertenecen al conjunto. Por lo tanto basta encontrar un sólo término de la sucesión que verifique |zn| > 2 para estar seguro que c no está en el conjunto.
La propiedad fundamental de los fractales es una cierta invariabilidad con relación a la escala, o dicho de otro modo, al acercarse a ciertas partes de la imagen reaparece en miniatura la imagen total. Un mismo motivo aparece a distintas escalas, a un número infinito de escalas.
No olvidemos que además de objetos matemáticos, fruto del duro trabajo (y a veces de la casualidad), los fractales son estructuras bellas. En este applet tenemos la oportunidad de recorrerlas y adentrarnos en sus profundidades. Así que disfruta introduciéndote y navegando por estos fractales.