El funcionamiento del espectrómetro
de masas (y del ciclotrón) se basa en dos apectos fundamentales, la
dinámica de partículas cargadas en el seno de campos eléctricos
y magnéticos, es por esto que estudiaremos en primer lugar el comportamiento
de dichas partículas cuando reciben la influencia de un campo eléctrico
y después en el caso homólogo en un campo magnético para
luego explicar el funcionamiento del espectrómetro una vez conocidos
los principios en los que está basado.
-Dinámica de partículas en un campo
eléctrico uniforme
Supongamos una partícula de carga
q y
masa
m conocidas situada en el interior de un campo eléctrico
E producido por una diferencia de potencial
∆V entre
dos placas conductoras. Considerando a la partícula en reposo aparece
sobre ésta una fuerza eléctrica
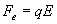
que, igualando a la expresión de la 2ª Ley de Newton obtenemos
m*(d2x/dt2) = q*E
de lo cual deducimos que la aceleracion de la partícula debido a la
acción del campo eléctrico es
a = q*E/m
Esta aceleracion producirá que la partícula,
partiendo del reposo, comience a desplazarse en la dirección y sentido
del campo eléctrico si consideramos positiva a la carga, esto es, en
el sentido en el que el potencial eléctrico entre las dos placas disminuye.
El potencial eléctrico en función del campo
se expresa (siendo el campo paralelo al eje Y) como
dV = -E*dy
y considerando constante el campo eléctrico, al integrar la ecuación
obtenemos que
∫
0V
dV = -∫0x E*dy →
V = -E*y
-Dinámica de partículas en un campo
magnético uniforme
Supongamos una partícula de las mismas características
que en el apartado anterior pero esta vez situada en una region del espacio
en la que existe un campo magnético
B y con una
velocidad
v. Teniendo en cuenta la expresión de la fuerza
de Lorentz
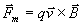
y considerando que las direcciones de la velocidad y el campo magnético
son perpendiculares, al igualarla a la 2ª Ley de Newton obtenemos
m*(d2x/dt2)
= q*v*B
y, por tanto, la aceleración será
a = q*v*B/m
Ahora la fuerza ejercida sobre la partícula será
perpendicular a la velocidad lo cual producirá que ésta varíe
en dirección pero no en módulo, por lo que, habiendo supuesto
que el campo magnético sea perpendicular a la velocidad, la partícula
describirá un movimiento circular uniforme, Esto quiere decir que la
aceleración obtenida anterirmente es centrípeta por lo que podremos
escribirla como
v2/r = q*v*B/m
y despejando
r obtenemos el radio de la circunferencia descrita
por la partícula
r = m*v/q*b