
Espectrómetro de masas
Planteamiento del problema
En esta practica, hemos realizado un estudio acerca del espectrómetro de masas. El problema que se nos plantea, es la necesidad de medir una relación entre carga y masa, en unas partículas atómicas dadas. Para ello usaremos un dispositivo, que nos permite determinar dichas masas de las partículas mediante un proceso en el cual usaremos las propiedades electromagnéticas de la carga y una campo que crearemos. La explicación de este sistema la desarrollaremos a continuación con detenimiento:

Resolución física
Para la resolución de nuestro problema, usamos distintas teorías físicas:
-Campo eléctrico: el campo lo vamos a usar para darle inducirle una velocidad a nuestra partícula a estudio, para ello someteremos la partícula a un potencial eléctrico, el cual inducirá energía cinética a nuestra partícula confiriéndole así una velocidad determinada de entrada al campo magnético en el que queremos realizar su estudio. Esta velocidad la averiguaremos mediante un análisis energético de la misma, para ello igualaremos ecuaciones de potencial y energía cinética,
despejando de esta igualdad nuestra velocidad.
-Campo magnético: para conseguir averiguar la masa de nuestra partícula a estudio, la someteremos a un campo magnético, y como todas las partículas llevaran la misma velocidad, el radio de curvatura que les inducirá el campo magnético mediante la fuerza de lorentz (ecuación 1), será distinto dependiendo de la masa de la partícula que estudiemos, luego el nombre que recibe de espectrómetro de masas, es por que el radio que obtenemos se obtiene mediante la impresión del espectro de nuestra partícula en una placa, de manera que podamos obtener el radio de curvatura, y poder relacionarlo así mediante la ecuación 2, a raíz de este resultado podremos obtener la relación carga masa, que necesitamos para cumplir nuestro objetivo, mediante la ecuación 3. Esto nos permitirá un estudio bastante completo acerca de nuestra partícula.
1)![]() 2)
2)![]() 3)
3)
Resolución numérica (programa)
Para construir nuestra resolución numérica, hemos creado un programa, que simula la entrada de la partícula en un campo magnético, para que esta experimente lo anteriormente explicado, y podamos así estudiar su supuesta masa. Para realizar un estudio numérico sencillo, hemos separado 3 partes claras del programa, para que cada una de ellas se ocupe de un movimiento concreto de la partícula, ya que esta pasara por tres fases bien diferenciadas:
-Primera parte:
esta
parte hace referencia al movimiento rectilíneo de la partícula. Las partículas
se someten a un proceso de ionización. Tras el proceso, dichas partículas se
someten a una diferencia de potencial, el cual las acelera a una velocidad muy
similar, y son arrojadas a un mismo punto mediante un sistema de rendijas. La
partícula no sufre fuerza alguna hasta que interactúa con el campo magnético,
por lo que describe un movimiento en línea recta, hasta la segunda parte del
programa. Esta expresión de movimiento rectilíneo la introducimos en el programa
como:
-Segunda parte: esta parte es el núcleo del programa, la cual es objeto de estudio y en la que centramos nuestro mayor interés. La partícula, tras el proceso descrito, avanza el línea recta y con una velocidad constante. Es en éste momento cuando es sometida a un campo magnético, el cual produce una fuerza en la partícula perpendicular a su velocidad dada por la ecuación de interacción magnética (Fuerza de “Lorentz”), esta evolución la expresemos mediante la siguiente sentencia:
El principio por el que averiguamos las masas se debe a que al llevar todas las partículas la misma velocidad, pero siendo estas de distinta masa (ya que el estudio se puede centrar en isótopos de un mismo elemento), los radios descritos por estos dentro del campo magnético serán distintos, dándonos una razón entre la masa y la carga, que viene a ser analizada en la siguiente parte del programa.
-Tercera parte:
en
esta parte determinamos el radio descrito por la partícula. Para ello calculamos
obtenemos el diámetro de la partícula cuando esta llega a la placa, a partir del
cual obtenemos el radio a estudio, y así mediante la siguiente sentencia
calculamos la razón que se nos pide como objetivo del estudio:
Además de obtener los resultados, esta parte será la que finalice el programa, deteniendo el movimiento de las partículas sometidas a estudio.
-Observaciones de interés: tenemos distintos comentarios u observaciones acerca del programa y las dificultados que hemos encontrado en su realización:
-Para la obtención de una masa aleatoria, utilizamos una función random propia del lenguaje del programa, la cual complica e incrementa el interés del trabajo, por que nos da masas de las cuales no sabemos nada y de las que tenemos que realizar el estudio.
-Para conseguir el funcionamiento de cada fase del movimiento de la partícula, introducimos una serie de condiciones "if" en el programa, las cuales alternan y modifican el tipo de interacción a la cual están sometidas las partículas dependiendo de que estén en una u otra posición, esta fue una de las mayores dificultades que encontramos, pues no conseguíamos que el tipo de interacción cambiara.
análisis de los resultados
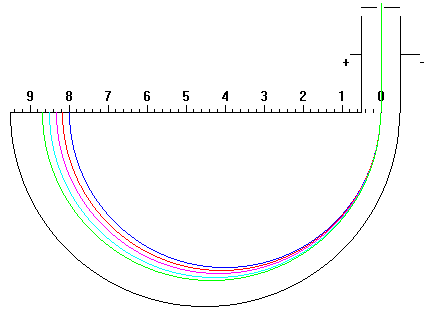
Al utilizar una función random, no podemos precisar si los resultados obtenidos son exactamente los esperados, aunque por lógica, se puede comprobar que la partícula de mayor radio calculado al final del programa, corresponde con aquella cuya masa es mayor, siendo a simple vista el radio mayor conforme a mayor masa resulta, por lo que consideramos que los resultados son positivos.
A continuación se puede ver todo lo comentado anteriormente en la siguiente simulación:
Algunos enlaces de interés son:
"Espectrómetro de masas por definición"
Copyright©Todos los derechos reservados