
PARADOJA DE LOS GEMELOS
Supongamos que en una familia hay dos hermanos gemelos. Uno de ellos coge su nave y viaja hacia una estrella que se halla a varios años luz de la Tierra. Realiza el viaje a una velocidad cercana a la de la luz. En el trayecto de ida y vuelta habrá envejecido menos y al llegar a la Tierra se encuentra con que su hermano tiene más edad que él.
La paradoja se encuentra en que hemos tomado dos marcos distintos de referencia. El hermano que se ha quedado en la Tierra podría decir que, desde el punto de vista del astronauta, es él quien se ha movido con la Tierra a una velocidad próxima a la de la luz y por tanto debería haber sido él quien hubiera envejecido menos que el astronauta.
Sin embargo, no existe paradoja alguna. Puesto que la nave del hermano que viaja está parada antes de salir, tendrá que acelerarla hasta alcanzar la velocidad deseada y, por tanto, no puede cumplir con la condición que dice que la velocidad ha de ser constante. Entonces, solo el hermano que se queda en tierra cumple con los requisitos para poder aplicar la teoría especial de la relatividad.

Para resolver nuestro problema partimos de la teoría de la relatividad, que se divide en dos teorías bastantes diferentes: la especial y la general. La teoría especial, desarrollada por Einstein y otros científicos en 1905, es la que utilizaremos, ya que se refiere a la comparación entre medidas realizadas en diferentes sistemas de referencia inerciales que se mueven con velocidad constante unos respecto a otros.
Albert Einstein, tras su estudio, postuló lo siguiente:
1.- Las leyes de la física pueden expresarse mediante ecuaciones que poseen la misma forma, en todos los sistemas de referencia que se muevan a velocidad constante unos respecto a otros.
2.- El valor de la velocidad de la luz en el vacío es 3x108 m/s, y no depende del observador que lo mide ni del movimiento de la fuente luminosa. Por tanto, esta velocidad es absoluta.
Einstein siguió el camino trazado por Galileo, lo aplicó a todas las leyes físicas y expuso que no podemos saber si la nave se mueve con relación a la Tierra o, por el contrario la Tierra con relación a la nave. Es decir, que el reposo no existe. El concepto de reposo queda eliminado con el primer postulado de Einstein. No hay experimento posible que nos indique si estamos moviéndonos a velocidad uniforme o si estamos parados.
La aportación clave de Einstein fue explicar que la única referencia inamovible es la velocidad de la luz, la cual siempre es la misma en el vacío, independientemente de si su fuente emisora se mueve deprisa, despacio o está parada. A partir de todo esto, Einstein sacó consecuencias espectaculares respecto al tiempo, la velocidad y el espacio.
Si tú tienes dos observadores que se encuentran situados en los sistemas de referencia O y O', éstos ubican de forma distinta en el espacio y en el tiempo un mismo suceso, según lo describan mediante la mecánica clásica o la mecánica relativista.
La transformación clásica o de Galileo es una transformación intuitiva, pero no cumple ninguno de los postulados de la relatividad. Por ello, necesitamos de las transformaciones de Lorentz que sí los cumple:
Tomando el sistema de referencia O, un suceso ocurre en una posición (x, y, z) y un instante t. Para el sistema de referencia O' el mismo suceso tendrá una posición y un instante determinados mediante las ecuaciones:

Vemos que el tiempo es diferente para cada sistema de referencia. Ya que buscamos las ecuaciones que permitan que la velocidad de la luz sea invariante del movimiento relativo de los observadores y, puesto que sabemos que la velocidad es la distancia dividida entre el tiempo, debemos ajustar las mediciones del tiempo y la distancia para los observadores en movimiento relativo.
Supongamos que la estrella A y la Tierra están fijos en el sistema del gemelo 1 (el que se queda en la Tierra). Despreciamos el movimiento de la Tierra. El gemelo 2 viaja a la estrella acelerando rápidamente hasta alcanzar la velocidad v, luego avanza con velocidad constante hasta llegar a la estrella. Es entonces cuando frena quedando momentáneamente en reposo respecto al gemelo 1. Para regresar, acelera de nuevo rápidamente hasta alcanzar la velocidad v hacia la Tierra, y viaja hasta llegar a ella, deteniéndose finalmente junto al gemelo 1.
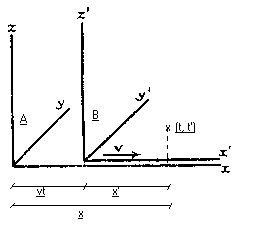
Podemos dividir el problema en dos sucesos, el primero cuando el gemelo 2 está en la Tierra y el segundo cuando llega a la estrella. Para el gemelo 1 los dos sucesos ocurren en tiempos y lugares distintos, sin embargo para el gemelo 2 aunque sean tiempos diferentes se producen en el mismo lugar, bajo sus pies.
Utilizando la transformación de Lorentz inversa para el tiempo y sabiendo que ambos sucesos ocurren en el mismo lugar respecto al gemelo 2, obtenemos la siguiente relación entre el tiempo medido por nuestros gemelos:

Como el factor (1-v 2 /c 2) 1/2 es menor que uno, la ecuación demuestra que el intervalo de tiempo medido entre dos sucesos por el gemelo 2 es menor que el medido por el gemelo 1 con respecto al cual el lugar en que se dieron los sucesos está en movimiento.
Definimos intervalo de tiempo propio como aquel entre dos sucesos que se dan en puntos que están en reposo con respecto a un observador; en nuestro caso, el gemelo 2.



Para concluir podemos afirmar que no existe paradoja alguna puesto que los papeles que desempeñan los gemelos no son simétricos: el gemelo 1 permanece en un sistema de referencia inercial pero el gemelo 2 tiene que acelerar si quiere volver a casa.
Queremos aclarar que sólo por razones estéticas vemos que el gemelo 2 se desplaza también en el eje Y, pero el problema es unidimensional.
Puede controlarla usando JavaScript. Por ejemplo, usando botones:
Enlaces a webs relacionadas:
Paula Bernal Molina paula.bernal@alu.um.es
Mª Elena Ros Bernabeu melena.ros@alu.um.es