Simulación del movimiento de un cuerpo en la superficie terrestre
Cuando lanzamos un cuerpo con una velocidad que forma un ángulo
con la horizontal, éste describe una trayectoria parabólica. En su obra
Dialogo sobre los Sistemas del Mundo (1633), Galileo Galilei expone que
el movimiento de un proyectil puede considerarse el resultado de
componer dos movimientos simultáneos e independientes entre sí: uno,
horizontal y uniforme; otro, vertical y uniformemente acelerado. Esto
tiene la ventaja de que podemos hacer los cálculos de forma
independiente en cada movimiento con sus ecuaciones correspondientes y
luego unirlos para obtener el dato que deseemos en el movimiento
complejo.
Para calcular las trayectorias de las partículas hemos empleado el método numético, es decir, a partir de la aceleración "integramos" numéricamente (y no analíticamente). Para emplear el método numérico calculamos el límite cuando la diferencia de tiempo(dt) tiende a 0 del cociente entre la diferencia de tiempo y la diferencia entre un instante final (vt+dt) y un instante inicial v(t). Al calcular el límite obtendríamos la aceleración. Para tiempos muy pequeños, sin embargo, hacemos la aproximación de que el límite será igual al cociente entre la diferencia de tiempo y la diferencia entre un instante final (vt+dt) y un instante inicial v(t). De esta forma, si conocemos la aceleración podemos obtener con gran facilidad el valor numérico de la velocidad. Si bien este valor es una aproximación, para dt suficientemente pequeños (por ejemplo dt=0.01) el resultado es bastante aproximado, y haciendo dt más pequeña podemos aproximarnos cuanto queramos.
Esto aplicado a nuestra simulación se traduce en que los movimientos en x y en y son de la forma:
En este caso concreto, dado que la aceleración es constante sería sencilla realizar, en vez de una integración numérica, una integración analítica de la aceleración, con lo que obtendríamos la velocidad, y la integración, también analítica, de la velocidad, para obtener la ecuación de la trayectoria. Comprendamos el punto de salida como origen de coordenadas. Si la velocidad de salida es v0 y el ángulo es á, tendremos que las componentes de la velocidad inicial son:
Para calcular las trayectorias de las partículas hemos empleado el método numético, es decir, a partir de la aceleración "integramos" numéricamente (y no analíticamente). Para emplear el método numérico calculamos el límite cuando la diferencia de tiempo(dt) tiende a 0 del cociente entre la diferencia de tiempo y la diferencia entre un instante final (vt+dt) y un instante inicial v(t). Al calcular el límite obtendríamos la aceleración. Para tiempos muy pequeños, sin embargo, hacemos la aproximación de que el límite será igual al cociente entre la diferencia de tiempo y la diferencia entre un instante final (vt+dt) y un instante inicial v(t). De esta forma, si conocemos la aceleración podemos obtener con gran facilidad el valor numérico de la velocidad. Si bien este valor es una aproximación, para dt suficientemente pequeños (por ejemplo dt=0.01) el resultado es bastante aproximado, y haciendo dt más pequeña podemos aproximarnos cuanto queramos.
a=lim((v(t+dt)-v(t))/dt) ----> Para dt próximo a 0 (muy pequeño) aproximamos -----> a=((v(t+dt)-v(t))/dt)
v(t+dt)=a*dt+v(t)
De la misma forma calculamos el espacio y obtenemos:
v=lim((x(t+dt)-x(t))/dt) ----> Para dt próximo a 0 (muy pequeño) aproximamos -----> v=((x(t+dt)-x(t))/dt)
x(t+dt)=v*dt+x(t)
x(t+dt)=v*dt+x(t)
Esto aplicado a nuestra simulación se traduce en que los movimientos en x y en y son de la forma:
vy = vy + a*dt; (a=g)
vx=vx; (ax=0)
y=y + vy*dt
x=x + vx*dt
Donde las velocidades iniciales son:
vx=v*cos(ang);
vy=v*sin(ang);
vx=vx; (ax=0)
y=y + vy*dt
x=x + vx*dt
Donde las velocidades iniciales son:
vx=v*cos(ang);
vy=v*sin(ang);
En este caso concreto, dado que la aceleración es constante sería sencilla realizar, en vez de una integración numérica, una integración analítica de la aceleración, con lo que obtendríamos la velocidad, y la integración, también analítica, de la velocidad, para obtener la ecuación de la trayectoria. Comprendamos el punto de salida como origen de coordenadas. Si la velocidad de salida es v0 y el ángulo es á, tendremos que las componentes de la velocidad inicial son:
vx0=v0·cos(ángulo)
vy0 = v0· sen (ángulo)
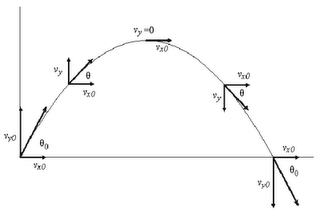
Dado que la aceleración es la de la gravedad (y la tomamos como
constante ya que el espacio recorrido por el cuerpo lanzado es
suficientemente pequeño como para tomar la superficie terrestre como
recta) tenemos que a=(ax,ay)=(0,-g). La composición de los dos
movimientos por el método analítico (calculando la integral) para la velocidad queda:
v=(vx, vy)=(vx0, vy0 + ay*t)=(v0*cos(ángulo), v0· sen(ángulo) - g*t)
La ecuación de la trayectoria, integrando la expresión anterior, será:
e=(x,y)=(x0 + vx0*t, y0 + vy0*t + (1/2)*a*(t^2))=(x0 +vx0*t, y0+vy0*t-(1/2)*g*(t^2))
No obstante debemos destacar el mayor interés que nos suscita el método de integración numérico, ya que nos permite definir todo tipo de trayectorias que estén sometidas a una aceleración, sólo con cambiar la aceleración. Si deseamos añadir por ejemplo una fuerza de rozamiento, lo único que deberíamos hacer es añadirle a "a" una aceleración en sentido contrario. a= g - b*v, y el resto lo mantenemos igual.
Es interesante destacar que en el punto más alto la velocidad en el eje y (debido a su fórmula) será 0. Si observamos la simulación vemos como esta velocidad va disminuyendo conforme nos acercamos al punto de máxima altura, donde su módulo es cero, y a continuación comienza a ser negativa.
También es interesante destacar que, aunque la velocidad y la aceleración no tienen la misma dirección (como se puede ver claramente en la simulación), las variaciones de dichas magnitudes sí tienen la misma dirección, ya que a=var_v/var_t
Dado que el movimiento parabólico posee una curvatura tiene una aceleración normal (que cambia el sentido del movimiento, es perpendicular al sentido del movimiento y apunta hacia el centro de curvatura) además de la tangencial (que cambia la velocidad del movimiento, tiene la misma dirección que la velocidad, y tiene su mismo sentido si la velocidad está aumentando, y contrario si está disminuyendo). La composición de la aceleración normal y la tangencial da como resultado la aceleración total que actúa sobre el cuerpo, en este caso g. Dado que en el punto más alto la aceleración tangencial es cero (porque la velocidad se mantiene constante (nula) en ese punto) toda la aceleración es normal, y por tanto la aceleración normal debe tener el valor de g. Gracias a ello podremos calcular el centro de curvatura con comodidad.
No obstante debemos destacar el mayor interés que nos suscita el método de integración numérico, ya que nos permite definir todo tipo de trayectorias que estén sometidas a una aceleración, sólo con cambiar la aceleración. Si deseamos añadir por ejemplo una fuerza de rozamiento, lo único que deberíamos hacer es añadirle a "a" una aceleración en sentido contrario. a= g - b*v, y el resto lo mantenemos igual.
Es interesante destacar que en el punto más alto la velocidad en el eje y (debido a su fórmula) será 0. Si observamos la simulación vemos como esta velocidad va disminuyendo conforme nos acercamos al punto de máxima altura, donde su módulo es cero, y a continuación comienza a ser negativa.
También es interesante destacar que, aunque la velocidad y la aceleración no tienen la misma dirección (como se puede ver claramente en la simulación), las variaciones de dichas magnitudes sí tienen la misma dirección, ya que a=var_v/var_t
Dado que el movimiento parabólico posee una curvatura tiene una aceleración normal (que cambia el sentido del movimiento, es perpendicular al sentido del movimiento y apunta hacia el centro de curvatura) además de la tangencial (que cambia la velocidad del movimiento, tiene la misma dirección que la velocidad, y tiene su mismo sentido si la velocidad está aumentando, y contrario si está disminuyendo). La composición de la aceleración normal y la tangencial da como resultado la aceleración total que actúa sobre el cuerpo, en este caso g. Dado que en el punto más alto la aceleración tangencial es cero (porque la velocidad se mantiene constante (nula) en ese punto) toda la aceleración es normal, y por tanto la aceleración normal debe tener el valor de g. Gracias a ello podremos calcular el centro de curvatura con comodidad.