En primer lugar nos centraremos en el movimiento del muelle tal y como está desarrollado en la simulación anterior, al que hemos añadido la fuerza de rozamiento. Para poder estudiar esto asignamos w=0, y b= coeficiente de rozamiento que deseemos, por ejemplo 0.2 si deseamos ver sus efectos lentamente. Si ponemos la simulación en marcha dando un valor de elongación podemos ver cómo el cuerpo, en llegar de llegar a la posición opuesta de la elongación inicial respecto a la posición de equilibrio, no la alcanza, y se va frenando a medida que avanza el tiempo, por lo que la amplitud del movimiento va disminuyendo progresivamente. La energía se va disipando por tanto debido a la fuerza de rozamiento.
Si ahora nos centramos en el efecto que produce la fuerza periódica sobre el sistema, veremos que, dependiendo de las condiciones iniciales que fijemos, la simulación tardará un cierto tiempo en comportarse como describiremos a continuación, a mayor elongación y menor fuerza de rozamiento tardaremos más en ver los efectos de la fuerza periódica. Esto es debido a que las condiciones iniciales se ven contrarrestadas por la fuerza de rozamiento. Cuando nosotros ponemos en marcha la simulación, si hay condiciones iniciales, se verán eliminadas al cabo de un tiempo y se comportará como describimos a continuación, si no hay condiciones iniciales, de forma inmediata ocurrirá lo siguiente. El sistema comienza a moverse debido a la fuerza armónica, sin embargo sobre él actúa también una fuerza de rozamiento. La energía mecánica será el resultado de la suma de las áreas de la potencia de la Fuerza armónica y de la Fuerza de rozamiento. éstas van fluctuando, la potencia de la fuerza de rozamiento es siempre negativa, la potencia de la fuerza periódica es a veces positiva, y a veces negativa. En cualquier caso conforme avance el tiempo ambas potencias tienden a ir compensándose, la energía total del sistema a veces crecerá, a veces decrecerá, pero lentamente irá tornándose constante (donde constante no es una línea recta, sino un movimiento ondulatorio de periodo constante con pequeñisima amplitud), conforme se estabilizan las potencias de las fuerzas. Todas estas fluctuaciones las podemos ver en la gráfica de la izquierda seleccionando las potencias de las fuerzas y la energía mecánica.
El sistema tiene una frecuencia de resonancia propia que es de la forma w^2= k/m (por ser un muelle). En nuestro caso, dado que m= 1 y k =1, la frecuencia es w=1. La resonancia es un fenómeno que se produce cuando un cuerpo se ve sometido a una fuerza periódica, cuyo periodo de vibración coincide con el periodo de vibración característico de dicho cuerpo. En estas circunstancias el cuerpo vibra, aumentando de forma progresiva la amplitud del movimiento tras cada una de las actuaciones sucesivas de la fuerza, de forma infinita si el coeficiente de rozamiento es = 0.
A la hora de experimentar con la simulación tenemos dos parámetros de gran importancia (ya que las condiciones inciales se ver atenuadas con mayor o menor rapidez), el coeficiente de rozamiento, y la frecuencia que le proporcionamos al cuerpo.
Cuando le proporcionamos al sistema una frecuencia que no es su frecuencia de resonancia, tenemos dos casos: si la frecuencia es menor que la frecuencia de resonancia, el cuerpo se mueve en fase con la fuerza armónica (en la gráfica, si seleccionamos la visión de la Fuerza Armónica y de la Posición de la partícula, vemos como están separadas 90º). Si la frecuencia es mayor, la partícula se moverá casi en oposición de fase (una diferencia de 180º). Si la frecuencia de la partícula es lo suficientemente alta, el cuerpo parecerá en reposo. Además la frecuencia, junto con la fuerza de rozamiento, influye en la amplitud del movimiento. Para una frecuencia igual a la frecuencia de resonancia será máxima, para una frecuencia mayor o menor, la frecuencia irá disminuyendo de una forma parecida a la siguiente curva (fijémonos en la curva de color rojo).
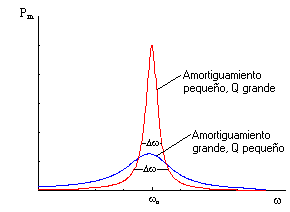
Si nos centramos en la fuerza de rozamiento, ésta influye, como hemos comentado, en la amplitud del movimiento. ¿Cómo? La respuesta está en la curva azul superior. A mayor fuerza de rozamiento, la curva de la frecuencia se achata, con lo cual podemos notar antes si el sistema está cerca de la frecuencia de resonancia, pero la amplitud que obtendremos con dicha frecuencia es mucho menor. Por el contrario si la fuerza de rozamiento es muy baja, los efectos de la resonancia se notarán sólo cuando nos encontremos muy cerca de dicha frecuencia, pero obtendremos una amplitud mucho más elevada. El caso límite es cuando la frecuencia es igual desde el primero momento a la frecuencia de resonancia y la fuerza de rozamiento es 0. En este caso teóricamente la amplitud aumentará indefinidamente, únicamente cuando w=w resonancia exactamente. Como nota podemos añadir que si la fuerza de rozamiento es superior a la fuerza de rozamiento crítica (w0/2), en este caso 0.5, entonces el sistema estará en equilibrio desde un primer momento, ya que la fuerza de rozamiento impedirá la oscilación.
En relación a la gráfica inferior derecha, ésta nos sirve para ver cómo se estabiliza la energía mecánica, y está representada la posición (en el eje x) frente a la velocidad (en el eje y). Legará un momento en que la elipse deje de aumentar de distancia respecto al origen y quede fija en una elpise. En ese momento el valor en el que la elipse corta con el eje x es el máximo valor de la amplitud, y el valor en el que corta con el eje de las "y" es el máximo valor de la velocidad,
El caso de la resonancia podemos verlo por ejemplo en el puente de Tacoma, en que el aire comenzó a vibrar a una frecuencia de un Hertzio contra la estructura del puente, muy poco aerodinámica.
Debido también a la resonancia una copa de vino puede romperse con notas muy agudas (de muy elevada frecuencia).