Partícula libre

El caso más simple es el de una partícula libre. La energía potencial E_p(x)=0

La ecuación de Schrödinger se escribe

Ecuación diferencial análoga a la de un movimiento armónico simple, su solución la expresaremos de otra forma equivalente 

Escalón de potencial 

El escalón de potencial consiste en una región x<0 en la que la energía potencial es nula, seguida de una región x>0 en la que la energía potencial es constante y de valor E₀. 

La función E_p(x) presenta por tanto, una discontinuidad en x=0.

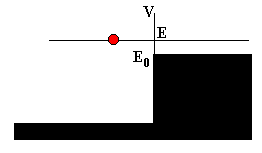
Se pueden presentar dos casos 

• Que la energía de la partícula sea mayor que la del escalón E>E₀.
• Que la energía de la partícula sea menor que la del escalón E<E₀.

Planteamos la ecuación de Schrödinger en cada una de las regiones y hallamos su solución de forma semejante al de la partícula libre. En la siguiente tabla se resumen los resultados.
 

Región x<0, Ep(x)=0	Región x>0, Ep(x)=E0

En el punto x=0, la función de onda Y debe ser continua y también lo debe ser su derivada primera.

Lo que da lugar a un sistema de dos ecuaciones con dos incógnitas que nos permiten expresar los coeficientes B y C en función del coeficiente A.

Veamos ahora el significado físico de los distintos términos de la solución de la ecuación de Schrödinger. En la primera región x<0 tenemos partículas incidentes y reflejadas, pero en la segunda región x>0 solamente tenemos partículas transmitidas. La función de onda tiene dos términos en la primera región y un solo término en la segunda.
 

Partículas	Función de onda	Probabilidad	Flujo
incidentes
reflejadas
transmitidas

Se denomina coeficiente de reflexión a la proporción de partículas incidentes que se reflejan

Se denomina coeficiente de transmisión a la proporción de partículas incidentes que se transmiten.

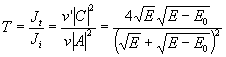
Como puede fácilmente comprobarse R+T=1

Podemos ver aquí, una analogía con el movimiento ondulatorio, una onda incidente al atravesar dos medios de distinta naturaleza (densidad, índice de refracción, etc., dependiendo del tipo de onda) da origen a una onda reflejada que se propaga en el primer medio, y a una onda transmitida que se propaga en el segundo medio.