Las expresiones para la impedancia en una línea de transmisión son de manejo un poco complicado. Una representación cartesiana de impedancias no es útil, sin embargo se observa que el coeficiente de reflexión es un vector complejo, de módulo menor o igual que la unidad, que gira cuando nos movemos a lo largo de la línea. Si se representa la impedancia normalizada sobre el plano del coeficiente de reflexión de voltaje, solamente necesitaremos un círculo de radio unidad.
|
ZN =
|
1 + Ro
----------
1 - Ro
|
En la carta de Smith se representa la impedancia normalizada sobre el plano del coeficiente de reflexión de voltaje.
Asignamos una notación de números complejos a Ro y ZN y sustituimos en la expresión anterior.
Ro = u + jv
ZN = rn + j xn
u + jv = (rn + j xn - 1 )/ (rn + j xn + 1 )
igualando partes reales e imaginrias:
rn (u –1) - xn v = -(u + 1)
rn v - xn (u –1) = -v
|
|
eliminando la parte reactiva rn
[u - rn /( rn + 1)]2 + v2 = ( rn + 1) -2
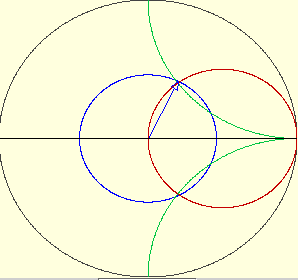
En coordenadas rectangulares de u y v, ésta es la ecuación de un círculo cuyo centro está localizado en u = rn /( rn + 1), v = 0 y cuyo radio es 1 /( rn + 1), circunferencia roja.
Si el procedimiento se repite, eliminando rn en lugar de un, el resultado es
(u – 1)2 + (v – 1/xn)2 = (1/xn)2
Serán circunferencias con centro en 1, 1/xn y radio 1/xn, en la figura arcos en verde.
En el siguiente enlace se puede ver un ejemplo de una
Simulación
realizada con
EJS.
