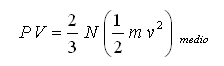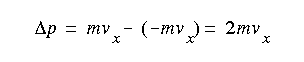
CONCEPTOS.
En nuestro modelo de gases ideales estos estan formados, como hemos visto en los anteriores apartados, por particulas que se mueven con una cierta energia cinética. La energía interna de un sistema, U, la definimos como la suma de las energías de todas las partículas que lo configuran mientras que la temperatura, T, viene relacionada con la energía media por partícula.
Al chocar las particulas entre si y con las paredes la energía es intercambiada de forma aleatoria entre todas las posibilidades de absorber energía que tiene la configuración atómica del sistema. En el caso de un gas ideal monoatómico, que es el sistema que hemos elegido por ser el más sencillo, la única forma de energía es la cinética de las partículas que lo forman, de modo que la temperatura en este caso esta directamente relacionada, como veremos, con la energia cinética media por partícula.
ECUACIÓN DE LOS GASES IDEALES.
De la experiencia primera y de la realizada en el apartado 2. PRESION llegamos a la conclusión de que para un gas que contenga N moléculas se cumple que: PV/T = Const, es la expresión conocida como ley de Boyle. También encontramos que la presión era proporcinal al número de partículas que forman el gas y a su temperatura. la constante de proporcionalidad la llamamos k.
A principios del siglo XIX Joseph Gay-Lussac repite las experiencias demostrando que esta relación es correcta independientemente del tipo de gas que se estudie.
Veamos una interpretación mas cuantitativa de la temperatura ayudándonos de la relación experimental encontrada conocida como ley de los gases ideales. En ella P es la presión, V el volumen, N el número de partículas, k la constante de Boltzmann y T la temperatura. Durante todo el siglo XIX nadie supo el número de partículas que hubiera en una cierta cantidad de gas, por lo que no tampoco podían calcular el valor de k.
En nuestro modelo cinético de gases ideales la presión que se ejerce sobre las paredes es debida al cambio en su cantidad de movimiento al chocar con las mismas. Tomando una particula que viaja con una componente x de su cantidad de movimiento y rebota en la pared volviendo con el mismo valor pero de signo opuesto la variación en la cantidad de movimiento sera:
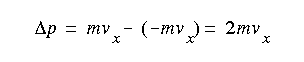
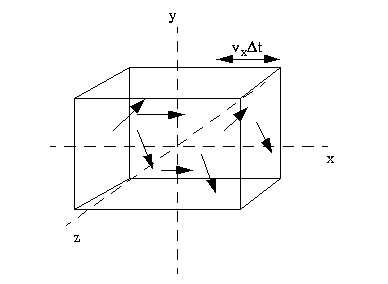
En la simulación observamos una partícula cuya velocidad solo tiene una componente, al chocar elásticamente con la pared de la derecha el vector velocidad invierte su sentido. Seleccionando gráfica observamos la variación de la cantidad de movimiento por intervalo de tiempo Δ t.
El número de moleculas que chocan con la pared en un intervalo de tiempo son aquellas que se encuentran a una distancia igual o inferior a
![]()
La variación total de la cantidad de movimiento de las moleculas del gas sera:
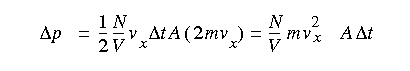
La fuerza ejercida sobre la pared sera la variación de la cantidad de movimiento por unidad de tiempo y la presion ejercida sera este valor dividido por el área de la pared A, y teniendo en cuenta que no todas las moléculas poseen el mismo valor de la componente x de la velocidad tomaremos su valor medio.
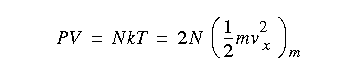
Donde hemos recordado la relación experimental entre P, V y T. De esta expresion deducimos que la energía cinética media asociada con el movimiento a lo largo del eje x es kT/2 como dicho eje no tiene ningun privilegio la energía asociada con los otros dos ejes también sera la misma por lo que podemos escribir: