Vamos a estudiar una función de forma completa
| (%i1) | f(x):=(x²-1)/(x-2); |
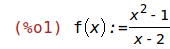
Dominio: f(x) no existe cuando el denominador se anula; por tanto lo igualamos a cero
y resolvemos la ecuación.
| (%i2) | solve([x-2=0], [x]); |
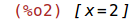
Por tanto, el dominio de f(x) es el conjunto de los números reales excepto 2. Veamos
a continuación si corta a los ejes; en primer lugar al eje Y, para esto calculamos f(0)
| (%i3) | f(0); |

Significa que la función pasará por el punto (0,1/2). Para el eje X hemos de resolver f(x)=0
| (%i4) | solve([f(x)=0], [x]); |
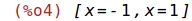
Pasa por los puntos (-1,0) y (1,0)
Se suele llamar "regiones" a los "trozos" donde la funcion es positiva o negativa. En este caso,
como la función es continua, salvo en los puntos que no están en el dominio, f(x) debe tener
signo constante entre los puntos en que se anula junto con los que no están en e dominio, es
decir entre -1, 1, 2. Para esto basta comprobar el signo en cada intervalo.
| (%i5) | f(-4); |

| (%i6) | f(0); |

| (%i7) | f(1/2); |

| (%i8) | f(3); |

Por tanto es negativa en (-infinito, -1) y positiva en el resto.
Estudiemos las asíntotas verticales
| (%i9) | limit(f(x), x, 2, minus); |
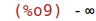
| (%i10) | limit(f(x), x, 2, plus); |

Esto significa que hay una asíntovartical en x=2.
Horizontales
| (%i11) | limit(f(x), x, inf); |

| (%i12) | limit(f(x), x, minf); |
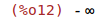
Por tanto no hay asíntotas horizontales.
Oblícuas
| (%i13) | limit(f(x)/x, x, inf); |
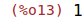
| (%i14) | limit(f(x)-x, x, inf); |
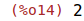
Luego la recta y=x+2 es asíntota oblícua.
Para estudiar el crecimiento hacemos la primera derivada y estudiamos su signo
| (%i15) | diff(f(x),x,1); |
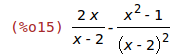
| (%i16) | ratsimp((2*x)/(x-2)-(x^2-1)/(x-2)^2); |
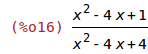
Para estudiar el signo de la derivada tenemos que estudiar por separado los signos
del numerador y el denominador para combinarlos. En este caso observamos que el
denominador es (x-2)² con lo que siempre es positivo y sólo hay que estudiar el signo del
numerador. Para esto buscamos sus raíces
| (%i17) | solve([x^2-4*x+1], [x]); |

| (%i18) | float(2-sqrt(3)), numer; |
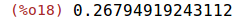
| (%i19) | float(2+sqrt(3)), numer; |
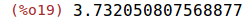
Para hacernos una idea de cómo son los números anteriores, hemos expresado en forma
decimal la raíces del numerador. Ya sabemos que entre dos raíces consecutivas no
cambia de signo. Sustituimos x en la derivada por valores comprendidos entre las raíces y
| (%i20) | subst(-2, x, (x^2-4*x+1)/(x^2-4*x+4)); |
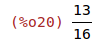
| (%i21) | subst(1, x, (x^2-6*x-21)/(x^2-6*x+9)); |

| (%i22) | subst(4, x, (x^2-6*x-21)/(x^2-6*x+9)); |
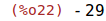
Esto significa que f(x) es creciente desde -infty hasta 2-sqrt(3) y decrece en el resto.
Ahora tenemos que estudiar los extremos. Recuerde que en los puntos en los que la
función pasa de creciente a decreciente hay un máximo y en los que pasa de decreciente
a creciente hay un mínimo; excepto en los puntos en los que no hay continuidad;
en nuestro caso x=2.
Entonces en 2-sqrt(3) hay un máximo que vale
| (%i23) | f(2-sqrt(3)); |
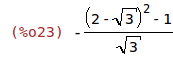
| (%i24) | float(-((2-sqrt(3))^2-1)/sqrt(3)), numer; |
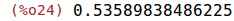
Por fin sólo nos resta una representación gráfica
| (%i25) | wxplot2d([f(x)], [x,-10,10], [y,-50,50])$ |
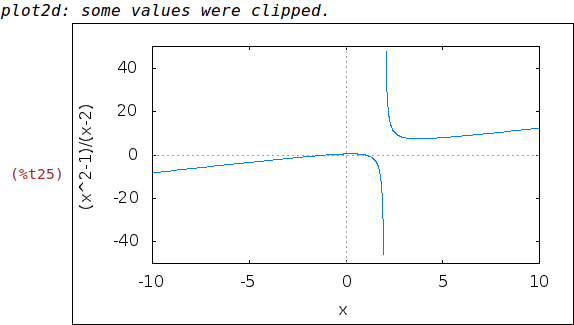
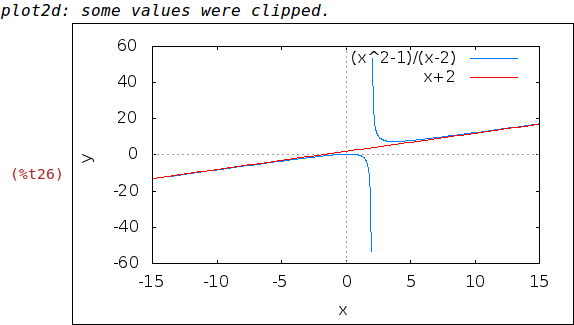
Podemos dibujar también la asíntota
| (%i26) | wxplot2d([f(x),x+2], [x,-15,15], [y,-60,60])$ |