Vamos a estudiar una función de forma completa
| (%i1) | f(x):=x*%e^(1/x); |
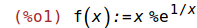
Dominio: f(x) no existe cuando el denominador del exponente se anula; por tanto el
dominio de f(x) es el conjunto de los números reales excepto 0. Veamos
a continuación si corta a los ejes; en primer lugar al eje Y, para esto deberíamos
calcular f(0), pero 0 no está en el dominio, por tanto no corta al eje Y.
Para ver si corta al eje X hay que hacer f(x)=0. Es evidente que esto sólo ocurriría si x=0 y no puede ser.
Se suele llamar "regiones" a los "trozos" donde la funcion es positiva o negativa. En este caso,
como la función es continua, salvo en el punto que no está en el dominio, f(x) debe tener
signo constante antes de x=0 y después. Para esto basta comprobar el signo en cada intervalo.
| (%i2) | f(-1); |
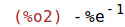
| (%i5) | f(1); |
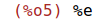
Por tanto es negativa en (-infinito, 0) y positiva en (0,+infinito).
Estudiemos las asíntotas verticales
| (%i6) | limit(f(x), x, 0, minus); |
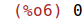
| (%i7) | limit(f(x), x, 0, plus); |
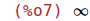
Esto significa que hay una asíntovartical en x=0, por la derecha y por la izquierda la función se acerca a 0.
Horizontales
| (%i8) | limit(f(x), x, inf); |
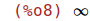
| (%i9) | limit(f(x), x, minf); |

Por tanto no hay asíntotas horizontales.
Oblícuas
| (%i10) | limit(f(x)/x, x, inf); |

| (%i11) | limit(f(x)-x, x, inf); |

Luego la recta y=x+1 es asíntota oblícua.
Para estudiar el crecimiento hacemos la primera derivada y estudiamos su signo
| (%i12) | diff(f(x),x,1); |
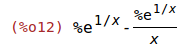
| (%i13) | ratsimp(%e^(1/x)-%e^(1/x)/x); |
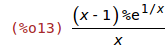
Para estudiar el signo de la derivada tenemos que estudiar por separado los signos
del numerador y el denominador para combinarlos. En este caso observamos que el
denominador es x, por tanto es negativo antes del cero y positivo después. El numerador
es producto de una exponenciaĺ, que siempre es positiva por (x-1), negativo antes del
uno y positivo después; así los puntos que tenemos son 0 y 1. veamos los signos.
Sustituimos x en la derivada por valores comprendidos entre 0 y 1.
| (%i15) | subst(-1, x, ((x-1)*%e^(1/x))/x); |
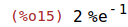
| (%i16) | subst(1/2, x, ((x-1)*%e^(1/x))/x); |

| (%i17) | subst(2, x, ((x-1)*%e^(1/x))/x); |
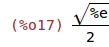
Esto significa que f(x) es creciente desde -infty hasta 0 y desde 1 en adelante; decrece en el resto.
Ahora tenemos que estudiar los extremos. Recuerde que en los puntos en los que la
función pasa de creciente a decreciente hay un máximo y en los que pasa de decreciente
a creciente hay un mínimo; excepto en los puntos en los que no hay continuidad;
en nuestro caso x=0.
Entonces en x=1 hay un mínimo que vale
| (%i18) | f(1); |
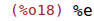
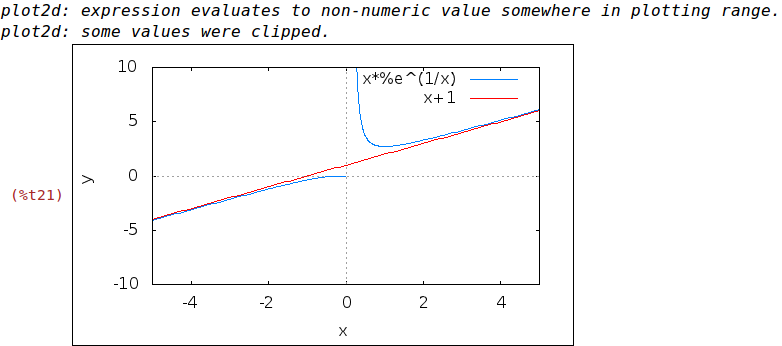
Por fin sólo nos resta una representación gráfica
| (%i20) | wxplot2d([f(x)], [x,-5,5], [y,-10,10])$ |
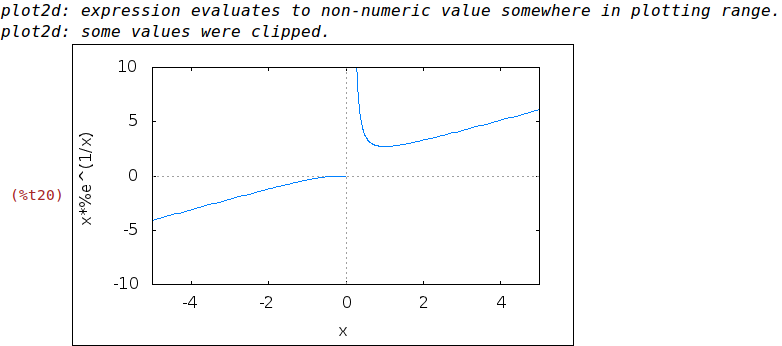
Podemos dibujar también la asíntota
| (%i21) | wxplot2d([f(x),x+1], [x,-5,5], [y,-10,10])$ |