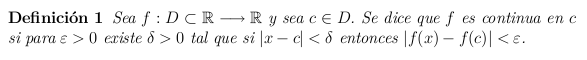
La continuidad de una función en un punto c de su dominio responde a la idea
de que los valores que toma f en los puntos cercanos a c están próximos al valor
f(c). Matemáticamente el concepto se formula del siguiente modo
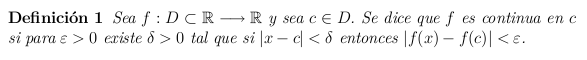
La continuidad es pues una propiedad que depende del punto c. Una función puede ser continua en un punto y no serlo en otros. Decir que una función es continua en un conjunto, como puede ser un intervalo, significa que la función es continua en cada uno de los puntos del intervalo.
En los estudios de la enseñanza media suele decirse que una función es continua en un intervalo «si es posible dibujarla sin levantar el lápiz del papel» lo cual, sin ser una definición matemática, ayuda a la intuición del significado de la continuidad en intervalos. Desde esa perspectiva Maxima, a través de su grafismo, podría ayudarnos a saber si una función es o no continua. ¿Le parece que las funciones sin(x), sin(1/x) y x*sin(1/x) son continuas en sus dominios mediante la visualización de sus gráficas? ¿Y la función parte entera que se obtiene con el comando entier?
La Definición 1 significa que fijado el punto c para cualquier valor positivo "epsilon" que nos den ha de existir un número positivo "delta" que cumpla lo que en ella se afirma. Geométricamente esto significa que para cada "banda" horizontal centrada en f(c) de altura "2*epsilon" ha de existir un número positivo "delta" de manera que los puntos del eje OX que distan de c menos de "delta" tienen su imagen por f contenida dentro de dicha banda horizontal.
Definimos el comando continua con cuatro variables: la función, el punto, epsilon y delta
Por ejemplo tomemos la función f(x)=1/x y el punto c=1. Nos dan epsilon=0.1 y buscamos valores de delta. Comenzamos haciendo delta=0.1.
Como se ve la gráfica no queda dentro de la banda horizontal correspondiente a epsilon=0.1 cuando tomamos delta=0.1. Pero podemos tomar un valor menor de delta y redibujar el resultado volviendo a ejecutar el código anterior.
Ahora el resultado es el adecuado; lo cual significa que para esos valores de f,c,epsilonel valor delta=0.05 (y cualquier otro menor) es adecuado, pero el valor delta:0.1 no lo es.
epsilon puede ser necesario disminuir el valor de delta aunque no cambien la función y el punto. Determínelo en el caso siguiente.
c aunque el valor de epsilon se mantenga puede requerir un valor de delta diferente. Determínelo en el caso siguiente.
En http://www.slu.edu/classes/maymk/Applets/EpsilonDelta.html puede encontrar herramientas con applet java que le permiten experimentar gráficamente el concepto epsilon-delta que aparace en el estudio de límites y continuidad.
Los ejemplos anteriores ponen de manifiesto que fijada la función f y el valor de epsilon, el valor de delta depende del punto. Un ejemplo bien sencillo es el de la función f(x)=x^2 en el intervalo [0,1].
Pero si cambiamos al punto c:1 ese valor de delta no sirve
y es necesario utilizar otro menor, como, por ejemplo, delta=0.02
La ventaja de este último valor de delta es que resulta válido para todos los puntos c pertenecientes al intervalo [0,2] (realice las experiencias necesarias hasta convencerse de ello).
¿Que tiene de especial el punto c=2? La gráfica siguiente puede ayudarle a dar respuesta a esta pregunta.
Si observa atentamente verá que, sin cambiar el valor de epsilon (ancho de la banda horizontal) el valor máximo admisible para delta en el punto 1/2 es mayor que el que corresponde al punto 2, siendo precisamente dicho punto el que necesita el menor valor de delta en todo el intervalo, de suerte que si elegimos dicho valor, nos va a servir para todos los puntos del intervalo[0,2].
Cuando, fijado epsilon es posible seleccionar una valor de delta que sirva para verificar la definición 1, sea cual sea el punto c se dice que la función es uniformemente continua.
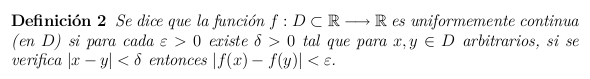
Con este lenguaje nuestros dibujos y reflexiones anteriores se podrían formular diciendo que la función f(x)=x^2 es una función uniformemente continua en el intervalo [0,2].
Esto es un caso particular de un teorema más general debido a Weierstrass que demuestra que toda función continua en un intervalo cerrado y acotado [a,b] es uniformemente continua.
Cuando el intervalo no es cerrado y acotado no puede darse una respuesta general: depende de la función.
Ejercicios
Basándose en el dibujo de las gráficas, y en las técnicas desarrolladas en esta sección, llegue a conjeturar (y si es capaz de hacerlo, demuestre su conjetura) qué puede afirmarse sobre la continuidad uniforme de las siguientes funciones
 |
 |