Primitivas e integrales

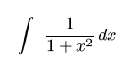
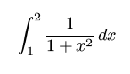
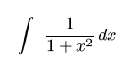
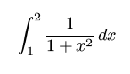
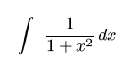Con el este símbolo estamos representando una función llamada primitiva de la función f(x):=1/(1+x^2) con la propiedad de que su derivada coincide con f. Seguramente usted sabe calcular la primitiva de f ¿verdad? Maxima también la sabe calcular. Utiliza para ello el comando

integrate(1/(1+x^2),x); tiene por primitiva cierta función, que se obtiene haciendo doble clik encima del texto resaltado en azul.

Para comprobar si la función arco tangente, que Maxima representa con atan(x), es la respuesta correcta podemos proceder a derivarla.

Como esta situación se da siempre, Maxima, de forma implícita, conviene con usted en que eludirá siempre esa constante. Pero... ¿a usted se le había olvidado la constante cuando le preguntamos si estaba de acuerdo con la respuesta de Maxima?

Vamos a complicar un poquito las cosas cambiando de función y tomando f(x):=1/(1+x^4). ¿Sabe calcular la primitiva de f? Le hacemos la misma pregunta a Maxima y obtenemos por respuesta

Si usted no tiene claro todavía como calcular por sí mismo la nueva primitiva, debería leerse con interés los contenidos teóricos del capítulo «Cálculo de primitivas» relativos a cómo hacer primitivas de funciones racionales, que así se llaman los cocientes de polinomios que puede encontrar en http://ocw.um.es/ciencias/analisis-matematico-i.

Pero volvamos a Maxima. Para saber si se ha equivocado o no lo que tenemos que hacer es derivar el resultado. Usted lo puede hacer «a mano» una vez que entienda el significado de la fórmula anterior que Maxima da como respuesta, y para ello lo único que necesita es saber que sqrt(2) significa raíz cuadrada de 2 y, más generalmente, que sqrt(x) representa la raíz cuadrada de x. ¡Pues manos a la obra! Es un buen ejercicio para usted tomar un papel y derivar la fórmula que Maxima nos ha proporcionado para, después de realizar las simplificaciones oportunas, llegar al resultado buscado.

Para Maxima realizar esos cálculos le lleva muy poco tiempo. Pero es que incluso no necesita que le escribamos con detalle la fórmula que tiene que derivar, porque él ya la conoce, es justamente la «última salida» que nos ha proporcionado y como siempre hace la representa con el símbolo % del tanto por ciento; de suerte que el resultado de derivar la última salida

- Tiene usted razón. Veamos si Maxima es capaz de simplificar esa endiablada fórmula de su «última salida» utilizando para ello un comando diseñado con esa finalidad

En efecto, Maxima tenía razón y esa era «la» primitiva, claro está, a falta de la constante.

Sería conveniente que usted realizara también esa misma tarea con lápiz y papel. ¡No sea perezoso, le conviene realizarla!

Integrales

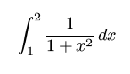Con este símbolo (que se lee integral de 1 a 2 de 1/(1+x^2)) representamos algo conceptualmente distinto de lo anterior: se trata de calcular el área bajo la curva de ecuación 1/(1+x^2) para x entre 1 y 2 cuya gráfica se puede obtener con la siguiente instrucción.

La estrategia para calcular el área bajo la curva conceptualmente es la misma que se utiliza para calcular el área de cualquier otra figura geométrica estudiada en el bachillerato: se elige primero la unidad de área (un cuadrado de lado unidad, generalmente) lo cual permite (utilizando la invariancia del área por movimientos rígidos de las figuras y el hecho de que el área de la unión de dos figuras disjuntas es la suma de las áreas de aquellas) asignar áreas a figuras como rectángulos, triángulos, trapecios... y a partir de dichas figuras asignar área a figuras que se puedan descomponer como uniones disjuntas (o al menos sin solapamiento) de figuras cuya área sepamos calcular.

Aunque no es este el momento de entrar en detalles, con los principios anteriores es posible asignar área a rectángulos cuyos lados tienen longitud racional, pero la fórmula del área de un rectángulo, uno de cuyos lados tiene longitud no racional, conlleva un proceso de aproximación sucesiva (o dicho de forma más precisa, de paso al límite) análogo al que vamos a utilizar para calcular el área bajo la curva anterior.

Dividimos el intervalo en dos partes iguales y consideramos rectas secantes a la curva como se muestra en la figura que sigue. Ello determina una poligonal sobre la curva y una colección de trapecios (dos en este caso) cuya área podemos calcular. Visualmente se aprecia que el área bajo la curva no es muy diferente de la suma de las áreas de dichos trapecios no solapados.

f(x):=1/(1+x^2)$ /* Definimos la función f */ n:2$ x(k):=1+k/n$ /* Definimos el número de intervalos, y sus coordenadas */ puntos_particion:create_list([x(k),f(x(k))],k,0,n)$ plot2d([f(x),[discrete,puntos_particion],[discrete,[1+1/n,1+1/n],[0,f(1+1/n)]]],[x,1,2], [legend, "f(x)","", "",""],[style,[lines,2,1],[lines,1,2],[lines,1,2],[lines,1,2]]);

En la fórmula anterior vaya incrementando el valor asignado a n y cerciorese visualmente de que la poligonal se aproxima progresivamente a la curva con la ventaja añadida de que el área bajo la poligonal es facilmente calculable por tratarse de una colección de trapecios (por claridad, sólo aparece pintado el primero de los n trapecios).

Es ahora el momento de calcular la suma de las áreas de dichos n trapecios. Recordemos para ello que el área de un trapecio es el producto de semisuma de las longitudes de sus bases (entendiendo por tales los lados paralelos, en este caso verticales) por la altura (en este caso horizontal de valor 1/n). Así pues la suma de las áreas de los n trapecios

n:10$ /* Fijamos con ello el número de subintervalos que usamos */ sum( (f(1+k/n)+f(1+(k+1)/n))/2 *1/n , k,0,n ),numer; que da como resultado .3412760634002064 para el valor de n

Posiblemente usted esté pensando que lo que acabamos de hacer es una complicación innecesaria para calcular el área bajo la susodicha curva ya que bastaría con haber aplicado la fórmula de Barrow, es decir haber hecho uso del siguiente

Teorema
Si f es una función continua, entonces existe una primitiva para f que denotaremos con F y para calcular la integral de f entre dos puntos a y b de su dominio basta con calcular F(b)-F(a).

Así que para calcular la integral de 1 a 2 de 1/(1+x^2) obtenemos una primitiva de 1/(1+x^2) mediante

y a continuación realizamos la evaluación de este resultado para x=2 y x=2 y calculamos su diferencia

En realidad no es necesario hacer las operaciones de cálculo de la primitiva y evaluación en los extremos del intervalo porque el comando integrate puede hacerlo directamente mediante

La razón de añadir numer en el código anterior es conseguir el resultado en formato decimal para poder compararlo con los resultados decimales antes calculados sumando las áreas de pequeños trapecios, que recordemos se realizaba con el código

Vaya incrementando el valor asignado a n y así poder comprobar como al aumentar dicho valor los resultados convergen hacia el que proporciona la fórmula de Barrow.

El ejercicio que hemos realizado comprueba, en un caso particular, la validez de la fórmula de Barrow. Pero dicha validez está garantizada por la demostración del teorema antes enunciado, que usted puede encontrar desarrollada en el capítulo «Cálculo integral» de las notas de clase, y que es aplicable a cualquier función que cumpla las condiciones señaladas.

Se trata de un teorema muy importante, conocido con el nombre de «Teorema fundamental del cálculo», porque relaciona dos cuestiones de naturaleza conceptual muy diferente: el problema inverso al de derivar, con el problema de calcular áreas bajo una curva.

Para darse cuenta de la importancia práctica del teorema, piense por un instante que hubieramos tenido que calcular el área anterior haciendo manualmente, con lápiz y papel, las sumas de las áreas de un importante número de trapecios. Pero más allá de su aplicabilidad en este ámbito, el teorema fundamental del cálculo es una herramienta teórica poderosa. Y por contra, es menos poderoso de lo que a primera vista puede parecer para calcular áreas.

Basta un instante de reflexión para convencerse de ello. Calcular áreas usando trapecios pequeños puede resultar tedioso y largo en el tiempo (aunque con una computadora el tiempo se mide de otra manera)... pero el camino está trazado y es posible recorrerlo para alcanzar el objetivo. En cambio poder hacer uso de la fórmula de Barrow requiere poder calcular antiderivadas y eso es muy difícil; de hecho las técnicas existentes sólo son aplicables a ciertos tipos muy particulares de funciones.

y tratamos de aplicar la fórmula de Barrow para calcular la integral en el intervalo [1,2] tenemos

y tratamos de hacer lo mismo, obtenemos un resultado rigurosamente correcto (hay que echarle un poco de imaginación para ver el símbolo de integral), pero diferente de lo que esperábamos

¿Como interpretar la respuesta de Maxima? Pues bien, lo que ocurre es que Maxima no sabe calcular una primitiva de la función sin(x)/x a la que luego poder aplicar la fórmula de Barrow. Quizá usted esté pensando, tal vez Maxima no es lo suficientemente bueno para calcular esa primitiva. Podría ser, pero no es el caso. De hecho nadie, ni humano ni máquina, va a ser capaz nunca de encontrar una fórmula en términos de las funciones habituales (llamadas, técnicamente, elementales). Aunque le pueda parecer una afirmación muy pretenciosa, créame, no lo es: hay un teorema que lo demuestra.

Si sólo dispusieramos de la poderosa fórmula de Barrow esto acabaría con la posibilidad de calcular la integral entre 1 y 2 de sin(x)/x, pero no es así porque podemos acudir a los trapecios

sum( (f(1+k/n)+f(1+(k+1)/n))/2 *1/n , k,0,n ),numer; que da como resultado una aproximación del área y al ir aumentando el valor de n converge hacia el valor del área buscada. Compruébelo usted mismo dando valores cada vez más grandes a n y repitiendo la ejecución del último código.

Si lo prefiere, Maxima puede hacerlo por usted muchas veces (30 por ejemplo) de forma rápida y sencilla:

Integración numérica: Método de Romberg

Desde un punto de vista teórico, la integral entre a y b de una función f continua (que supondremos positiva por sencillez, aunque eso es irrelevante) se determina calculando el límite de las sumas de areas de trapecios correspondientes a poligonales obtenidas subdiviendo el intervalo en subintervalos cuya longitud tiende a 0. Y eso es lo que hemos aplicado en la sección anterior. Desde un punto de vista práctico se plantea el problema de cómo elegir los puntos de división del intervalo o cuantos puntos tomar para obtener una respuesta satisfactoria en términos de computación.

Esa es una cuestión de Análisis Numérico que excede el objetivo de estas notas. Simplemente señalaremos que existe un «Método de Romberg» para evaluación de integrales (véase, por ejempo, http://es.wikipedia.org/wiki/M%C3%A9todo_de_Romberg) que Maxima tiene implementado con un comando romberg cuya sintaxis es similar a la del comando integrate. Veamoslo aplicado al ejemplo que hemos estado considerando anteriormente.