
Para un matemático una sucesión es una aplicación del conjunto N de los números naturales en el conjunto R de los números reales.
Dicho de otro modo eso significa una «lista» de parejas [n,a[n]] donde el primer elemento n de la pareja es un número natural que indica la posición en la lista y el segundo a[n] el valor que tiene dicho término n-ésimo de la lista.
Una fila de personas, cada una con su altura a[n] podría ser modelada matemáticamente por una sucesión. Bien es verdad que una sucesión matemática abstracta tiene siempre una cantidad infinita de términos mientras que una tal fila tiene un número finito de personas.
Obsérvese que no hemos dicho que las personas estén ordenadas de acuerdo a su altura. Están ordenadas sí, pero de acuerdo con su posición en la fila, no de acuerdo con su altura.
A continuación mostramos algunos ejemplos de sucesiones. Maxima puede escribir los términos que deseemos, pero siempre en una cantidad finita (el infinito es una abstracción que sólo tiene existencia en la mente). Comenzamos utilizando el comando kill para eliminar de la memoria todas las definiciones que pudiéramos haber realizado con anterioridad a fin de evitar resultados extraños y luego hacemos uso del comando makelist que permite construir listas como las que nos interesan.
a[n] así definida, que son Cambie el número de términos y experimente con la sucesión anterior construyendo listas más largas. Nunca podrá tener de forma «actual» la lista completa, pero «potencialmente» sí la tiene y sin ambiguedades, en cuanto que es posible conocer el valor a[n] de cualquier término de la lista.
¡Eso es lo característico de una sucesión!
En una sucesión el valor del término n-ésimo está definido siempre de forma inequívoca. Pero hay sucesiones, como la anterior, para las que es posible obtener de forma inmediata el valor del término n-ésimo, mientras que en otras dicho valor depende de los valores anteriores de los términos de la sucesión.
Por ejemplo, pensemos en una sucesión cuyos dos primeros términos son a[1]=0, a[2]=1 y los restantes términos, para n>2, se obtienen como la media aritmética de los dos términos inmediatamente anteriores; o dicho de otra manera, a[n]:=(a[n-1]+a[n-2])/2
a[n] así definida, que le serán mostrados en la ventana superior de xMaxima cuando ejecute el código
Como en el caso del ejemplo precedente, Maxima puede calcular sin dificultad el término 100
Para usted, calcular a[100] en la sucesión del Ejemplo 1 es inmediato; para el Ejemplo 2 también podría determinar sin ambiguedad (salvo error de cuentas) el valor de dicho término, pero tendría que trabajar mucho más, porque necesitaría calcular previamente todos los anteriores.
El Ejemplo 2 es una muestra de que se conoce con el nombre de sucesiones recurrentes. Las sucesiones recurrentes son más frecuentes de lo que a primera vista pudiera parecer. Y muy antiguas: busque en la wikipedia «Sucesión de Fibonacci»
Si realiza la búsqueda anterior podrá encontrar que la sucesión de Fibonacci es la solución a un problema de la cría de conejos. También encontrará allí que, en este caso, es posible obtener una fórmula para a[n] sólo en términos de n, lo cual hace, para usted, más sencillo el cálculo del valor de a[1000]. También encontrará otras informaciones curiosas relacionadas con esta sucesión.
La definición de límite de una sucesión formaliza la idea intuitiva de que los valores de la sucesión a[n] según va avanzando n se van acercando a cierto número real L que se llama el límite de la sucesión. Prescindimos aquí de la definición formal que podrá encontrar más adelante.
En cada uno de los ejemplos siguientes construya la lista finita de los términos de la sucesión (debe añadir el código necesario inspirado en los ejemplos precedentes) y conjeture si tienen o no límite y caso de tenerlo cúal es su valor. Obsérvese el valor que asignamos al comando booleano numer para conseguir resultados decimales.
Para la sucesión del Ejemplo 4 tendrá que hacer varios cálculos. Sea reflexivo y compare los primeros términos de la sucesión con los términos muy avanzados hasta que intuya cual debe ser el valor aproximado del límite.
En el Ejemplo 5 aparece una sucesión recurrente. Puede comprobar experimentalmente que se trata de una sucesión monótona con lo cual para que tenga límite basta con que está acotada, lo cual también puede experimentar usando Maxima
a el valor del límite ha de verificarse la ecuación a=1-sqrt(1-a) lo cual permite calcular el valor de a. ¿Era ese el valor que usted había conjeturado? Calcule el límite de la sucesión a[n+1]/a[n].
Un par de nuevos ejemplos para que analice la existencia del límite y calcule su valor.
Aunque la estrategia utilizada en el Ejemplo 5 es muy útil para calcular el límite de una sucesión recurrente, no siempre es tan sencillo. El Ejemplo 8 es una buena muestra de ello porque llegaríamos a la ecuación a=(a+a)/2 que no permite determinar el valor de a. No obstante los rápidos cálculos que Maxima realiza nos puede ayudar a darnos cuenta de que el límite debe existir y a conjeturar el valor del mismo. Aquí recurrimos al grafismo para visualizar la sucesión, que, en última instancia es una aplicación de los naturales en los reales. Al hacerlo nos percatarnos de que aunque globalmente no es una sucesión monótona, la sucesión de sus términos pares e impares si lo son y que parece verificarse una relación del tipoa[2*n-1]<a[2*n]<a[2*n+1]<a[2*n+2]. Esa es la clave para demostrar de forma abstracta la existencia del límite y calcular su valor.
Decíamos en el apartado anterior que la definición de límite de una sucesión formaliza la idea intuitiva de que los valores de la sucesión a[n] según va avanzando n se van acercando a cierto número real a que se llama el límite de la sucesión.
Si lo piensa un poco se dará cuenta que la idea de «se van acercando» es bastante imprecisa: el 1 y el 1.1 ¿están cerca o lejos?, ¿qué puede decir sobre el 1 y el 1'001? Estar cerca no es algo absoluto, es algo relativo. El 1 y el 1'001 pueden estar cercanos si nuestro aparato de medida sólo es capaz de medir las centésimas, porque no podremos distinguirlos, pero si nuestro aparato es capaz de medir con una precisión de millonésimas el 1 y el 1'001 no están cerca: están lejísimos el uno del otro.
En libros antiguos puede encontrarse la expresión «se va acercando tanto como se desee» con lo que se trataba de evitar ese carácter relativo de la cercanía. La definición matemática de límite

es muy precisa. Si me das cualquier «epsilon», lo cual viene a significar «dame tu nivel de precisión», entonces existe una posición en la lista (el valor n0) tal que a partir de ella los términos a[n] de la sucesión están cercanos al límite a, para el orden de precisión que me has fijado.
Veamos a continuación el significado geométrico de la definición de límite. Lo haremos con una sucesión concreta, a[n]:=n/(n+5)$, pero usted puede fácilmente cambiar de sucesión y realizar sus propias experiencias. Observemos que la definición sólo se ocupa de saber si algo es o no el límite, no es una técnica de cálculo del «candidato» a límite. Comenzaremos buscando nuestro candidato mediante experimentación.
Incrementamos el número de puntos poniendo en el código anterior, por ejemplo, m:100 luego m:1000... Parece claro que el límite es 1.
Vamos a aplicar la definición: tenemos la sucesión, nuestro candidato a límite y vamos a fijar un valor de «epsilon», por ejemplo 0.1. La cuestión existe n0 y cual es un valor admisible para él
Con el valor asignado m:10 no vemos nada en el gráfico: los 10 primeros puntos no están cerca de 1. Vayamos subiendo el valor de m de 50 en 50... ¿qué ocurre? Pues que con posterioridad al término 50 (quizá un poco antes) todos están cerca de 1: son ellos los que aparecen en la pequeña ventana horizontal que recorta la elección del rango de valores de y que hemos seleccionado. Para ese epsilon, 50 es un valor adecuado para n0, pero también lo es 100... la definición no habla de buscar el menor sólo saber que existe uno que verifica las condiciones.
Elija otro valor de «epsilon» y vuelva a calcular un n0... repítalo cuantas veces quiera, seguro que siempre encuentra el n0. Ese es el significado de la definición. Haga experiencias con otras sucesiones.
Focalizar en una pequeña banda horizontal en torno al candidato es lo esencial... pero tienen que estar «casi todos» los términos dentro la banda (sólo puede haber un número finito fuera) para no engañarse. Por ello no sólo hay que mirar en la banda, hay que mirar también en todo el eje vertical. Observe lo que puede suceder
¿Está seguro de cual es el límite de la sucesión anterior? Suprima el código que limita la banda y vuelva a dibujar. Seguramente ahora comprenderá perfectamente porqué una sucesión sólo puede tener un límite.
El reto. Trate de hacer algo similar a lo anterior con la sucesión a[n]:=(1+1/n)^n. Lo primero es buscar un candidato a límite; luego ver que nuestro candidato es realmente el límite.
Las secciones anteriores estaban encaminadas a adquirir las nociones de sucesión y límite. Pero Maxima permite calcular mediante un comando el límite de ciertas sucesiones cuyo término general pueda expresarse como una fórmula explícita de n. La sintaxis es muy simple
inf); como se muestra en los ejemplos que aparecen a continuación.
Con inf indicamos que n tiende a infinito. En realidad esto es obvio: en las sucesiones n siempre tiende a infinito. La razón de incluirlo aquí se debe a que el límite de funciones utiliza la misma sintaxis y en tal caso la variable no siempre tiende a infinito.
Obsérvese que Maxima conoce el «número e» que él representa en la forma %e.
Con este comando podemos calcular límites como el de Ejemplo 4 de forma exacta, y no aproximada como hacíamos dando valores a n. Pero nuestra conjetura de entonces resulta ser cierta.
Ejercicios
1. Trate de calcular con Maxima los siguientes límites. Realice listas finitas de los términos y el gráfico correspondiente.
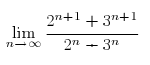
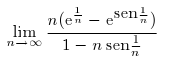
2. Utilice Maxima para conjeturar que las siguientes sucesiones recurrentes tienen límites. Luego calcule rigurosamente su valor, suponiendo que existe, y compare dicho valor con las aproximaciones numéricas obtenidas con Maxima.
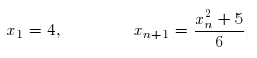
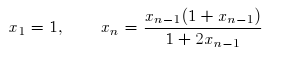
3. En la imagen se muestra la gráfica de la función f(x)=x^2 y el área de la región en amarillo coincide con el valor de la suma de Riemann correspondientes a una partición del intervalo [0,2] en 16 subintervalos iguales. Escriba la fórmula de la sucesión S[n] correspondiente al valor de la suma de Riemann con n intervalos y calcule el valor de dicho límite utilizando Maxima. Utilice también el comando integrate de Maxima, que calcula integrales definidas, para comparar los resultados.
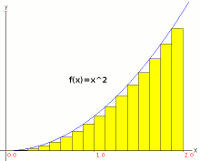
Gráficas de este tipo pueden construirse desde la página www.slu.edu/classes/maymk/Riemann/Riemann.html
 |