Explicación física del problema

    El problema que se nos planteaba era ver como se propaga una onda electromagnética en el espacio, de tres dimensiones. Para ello contábamos con las ecuaciones de Maxwell de las que se deduce que cambios temporales en el campo magnético producen cambios espaciales en el campo eléctrico 

En un sistema de coordenadas de tres dimendiones  tenemos un campo eléctrico en la dirección del eje x , y un campo magnético en la dirección del eje y.

Para solucionar el problema dividimos el eje z, que tiene una longitud L en N partes iguale, cada una de esas partes tendrá una longitud dz.Vamos a calcular el campo eléctrico en cada instante en los puntos del 0 al i, es decir:zE1,zE2,...,zEi. Inicialmente le asignamos al campo eléctrico en todos los puntos el valor 0. 

También hemos dividido el eje z tal que los intervalos tienen la misma longitud que antes, dz, de manera que tenemos localizados los puntos donde queremos calcular el campo magnetico entre los puntos donde queremos calcular el campo eléctrico.  E inicialmente le asignamos alcampo magnético en todos los puntos 0

En la página de inicialización hemos puesto:

for(int i=0; i<=N;i++){
zE[i]=i*dz;
Ex[i]=0;
}
 
for(int i=0; i<N;i++){
zB[i]=(i+0.5)*dz;
By[i]=0;
}

Inicialmente sólo  tenemos un campo eléctrico en el punto 0 cuyo módulo vale A.sen(5.t) y va en la dirección del eje x.Como se puede observar el módulo varía con el tiempo, pero la dirección es siempre la misma. Lo que hacemos es calcular en cada momento cuanto vale el módulo del campo eléctrico.

 Ahora que ya tengo las condiciones iniciales, viene el proceso de propagación de los campos. Vamos a calcular los campos en cada punto según avance el tiempo utilizando las ecuaciones de Maxwell. Para calcular el campo magnético en cada punto utilizamos la ley de Faraday, que nos dice que cambios espaciales o de magnitud del campo eléctrico, provocan la aparición de un campo magnético, que depende de las variaciones del campo eléctrico.

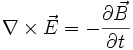
    Como en nuestro caso sólo tenemos campo eléctrico en la dirección x, sería: ∂ Ex /∂z = -∂By/ ∂t

    En vez de tomar diferenciales tomamos intervalos: ∆ Ex /∆z = -∆By/ ∆t

 Para calcular ahora el campo elécrico utilizaremos la ley de Ampere-Maxwell para el vacío, ya que la onda no se propaga por ningún medio, sino que en el vacío:

Pero como:   y entonces la ley de Ampere-Maxwell quedaría como:

Y como nosotros los estamos haciendo con intervalos la formúla quedaría como:

En la página de evolución tenemos:

t=t+dt;
Ex[0]=A*Math.sin(5.*t);
 
 
for(int i=0;i<N;i++){
By[i]=By[i]- ((Ex[i+1]-Ex[i]) * (dt/dz));
}
 
EN1=Ex[N-1];
for(int i=0;i<N-1;i++){
Ex[i+1]=Ex[i+1]- ((By[i+1]-By[i]) * dt*c*c/dz);
Ex[N]=Ex[N]-(Ex[N]-EN1)*dt*c/dz;
}