En esta simulación hemos representado el movimiento de un cuerpo cuando se ve sometido a una aceleración que, en lugar de ser constante (como en la simulación anterior) varía en función de un parámetro (en este caso x, la elongación).
El movimiento de un cuerpo es descrito mediante la determinación de su aceleración, su velocidad y su posición en función del tiempo. En este caso la aceleración no supone ningún problema, ya que viene dada por la fórmula (teniendo en cuenta que tomamos una partícula de masa 1):
ax = -K*x
También hemos añadido una gráfica en la que podemos ver la
variación de la energía potencial (en rojo) y la energía cinética (en
verde) alrededor del punto de equilibrio (en nuestro caso el 0, es
decir, la posición inicial de la partícula antes de ser estirada)
respecto a la energía potencial del sistema (una parábola de fórmula
k*x^x/2, como veremos más adelante). Gracias a la parábola podemos
apreciar la relación entre Energía cinética y potencial que comentamos
más adelante. También podemos ver una recta de color amarillo que
representa la energía total del sistema (la suma de la energía cinética
y la potencial en cada punto), y que como podemos ver es constante ya
que no actúan otras fuerzas. En la próxima simulación podremos agregar
una fuerza de rozamiento a este movimiento oscilatorio y ver cómo la
energía total del sistema se va disipando.
Para calcular la velocidad, dado que la aceleración no es constante, empleamos el método numérico utilizado en la simulación del movimiento de un cuerpo en la superficie terrestre. El método numérico consiste en calcular el
límite cuando la diferencia de tiempo(dt) tiende a 0 del cociente entre
la diferencia de tiempo y la diferencia entre un instante final (vt+dt)
y un
instante inicial v(t). Al calcular el límite obtendríamos la
aceleración. Para tiempos muy pequeños, sin embargo, hacemos la
aproximación de que el límite será igual al cociente entre la diferencia de tiempo y la diferencia entre un instante final (vt+dt) y un instante inicial v(t).
De la misma forma calculamos el espacio y obtenemos:
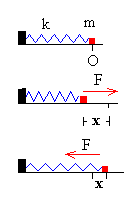
Si nos centramos en nuestra simulación, en ella podemos apreciar el movimiento de una partícula cuyo extremo está sujeto a un muelle cuando sobre ella actúa una fuerza. La fuerza que produce la aceleración es proporcional al desplazamiento (x) y de sentido contrario a éste. Cuando soltamos la partícula tras producir un cambio en su posición ésta empieza a oscilar.
a=lim((v(t+dt)-v(t))/dt) ----> Para dt próximo a 0 (muy pequeño) aproximamos -----> a=((v(t+dt)-v(t))/dt)
v(t+dt)=a*dt+v(t)
De la misma forma calculamos el espacio y obtenemos:
v=lim((x(t+dt)-x(t))/dt) ----> Para dt próximo a 0 (muy pequeño) aproximamos -----> v=((x(t+dt)-x(t))/dt)
x(t+dt)=v*dt+x(t)
Si nos centramos en nuestra simulación, en ella podemos apreciar el movimiento de una partícula cuyo extremo está sujeto a un muelle cuando sobre ella actúa una fuerza. La fuerza que produce la aceleración es proporcional al desplazamiento (x) y de sentido contrario a éste. Cuando soltamos la partícula tras producir un cambio en su posición ésta empieza a oscilar.

Si nos centramos en el panel del centro,
podemos ver las representaciones de la velocidad, la aceleración y la
posición (dependiendo de cual elijamos), pudiendo ver simultáneamente
el vector correspondiente a la gráfica sobre el cuerpo en movimiento.
Como podemos apreciar las tres magnitudes son representadas como
movimientos armónicos, esto es, movimientos que dependen de una
magnitud seno o coseno. Podemos comprobar esto a través de la obtención
analítica de las expresiones correspondientes a las tres magnitudes:
Aplicamos la segunda ley de Newton al sistema formado por la partícula de masa m y el muelle de constante k. Fuerza = ma = -kx
ma=-kx
Expresado en forma de ecuación diferencial
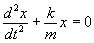
Esta es la ecuación de un movimiento armónico simple de frecuencia angular
w 2=k/m
y periodo
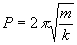
La posición x de la partícula viene dada en función del tiempo t por al ecuación
x=A·sen(w ·t+j )
donde A, j y w se determinan a partir de las condiciones iniciales: posición inicial y velocidad inicial de la partícula.
La velocidad v de la partícula se obtiene derivando x respecto del tiempo
v=A·w ·cos(w ·t+j )
La aceleración a se obtiene derivando la velocidad v respecto del tiempo
a=-A·w2·sen(w ·t+j )=-w 2·x
La energía cinética de un sistema es una magnitud que mide la variación del módulo de la energía Ec= 1/2*m*v^2. (Donde v^2 = v*v ->producto escalar de vector velocidad por sí mismo, en nuestro caso en una sóla dimensión). La definición de energía cinética la realizamos a partir de calcular el trabajo entre un punto A y un punto B realizado por una fuerza F, al valor de dicho trabajo lo denominamos variación de la Energía cinética.
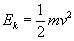
La energía potencial la obtenemos cuando calculamos el
trabajo de una fuerza conservativa (aquella fuerza cuyo trabajo no
depende de la trayectoria, por ejemplo el peso). Definimos variación de
energía potencial con signo negativo al trabajo realizado por una
fuerza conservativa desde un punto A a un punto B. La energía potencial
podemos obtenerla por tanto con facilidad integrando la fuerza que
actúa sobre dicho cuerpo respecto a la posición, y depende del tipo de
fuerza, por lo que la energía potencial gravitatoria es diferente, por
ejemplo, de la energía potencial elástica.
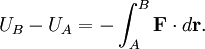
La energía potencial en nuestro caso es
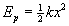
dado que F=-k*x. (Realizamos la integral de la fuerza analíticamente, y le cambiamos el signo).
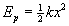
dado que F=-k*x. (Realizamos la integral de la fuerza analíticamente, y le cambiamos el signo).
Como nota final deseo animar al lector a que experimente con la simulación y cambie el parámetro K y la elongación. Podrá apreciar cómo aumenta o disminuye el periodo de oscilación en el primer caso, y cómo aumenta o disminuye la posición a la que llega la partícula en el segundo caso. Es también muy interesante la visualización de cómo cambian la velocidad y la acelerezación a medida que la partícula oscila.