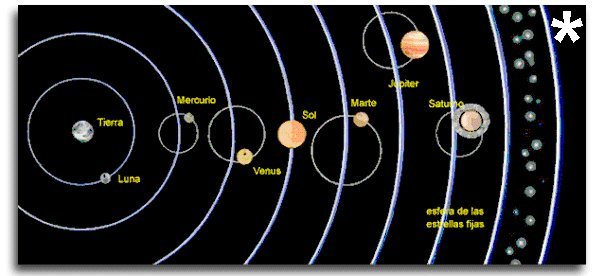
Fig.1 Representación del modelo ptolemaico.
Cuando observamos a Marte durante una noche estrellada podemos comprobar que muestra un comportamiento especial, diferente al resto de los objetos estelares: se desplaza a través del campo estrellado. Esta característica, que comparte con el resto de los planetas fue observada ya por los griegos, que llamaron a estos cuerpos planetas que puede traducirse por errantes.
Si observamos el movimiento de Marte sobre el fondo de estrellas y representamos su posición sobre un atlas estelar noche tras noche podremos determinar que su movimiento a traves de la eclíptica no es constante sino que en ciertas ocasiones parece detenerse e incluso dar marcha atras para, posteriormente, recuperar su dirección anterior. En otras palabras, Marte realiza un bucle en el espacio.
Este hecho (que se da también para el resto de los planetas exteriores), que era bien conocido en la antiguedad clásica, dio lugar a multidud de modelos astronómicos que intentaban describir estos extraños movimientos de una forma racional. De todos estos modelos, el que más prosperó y fue posteriormente aceptado por la filosofía cristiana de la Edad Media fue el ptolomeico que añadía al movimiento de los planetas alrededor de la Tierra, dos movimientos llamados epiciclos y deferentes que suponían que cada planeta exterior realiza un movimiento circular alrededor de su propia esfera.

Mediante este sistema era posible explicar los extraños movimiento de Marte y del resto de los planetas. La siguiente animación muestra a Marte girando alrededor de la Tierra (que en el sistema geocéntrico es considerada estática) y a su vez realizando un movimiento de epiciclo.
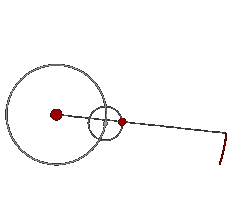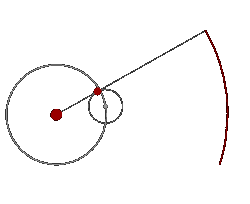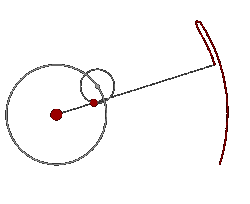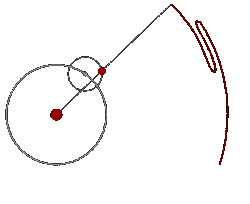
Este modelo permaneció inmutable hasta la época de Keppler, que basándose en las precisas observaciones de Tycho Brahe, dedujo sus tres leyes fundamentales del movimiento de los planetas, explicando de esta forma los motivos reales de estos extraños bucles.
La explicación no es otra que el hecho que la Tierra gira alrededor del Sol más rápido que el resto de los planetas exteriores, de forma que cada cierto tiempo, adelanta a Marte (y a los otros planetas). Visto desde la Tierra, nos parece que es Marte el que se detiene y retrocede.
Para calcular el movimiento relativo de Marte con respecto a la Tierra, solo tenemos que calcular el vector posición que une a la Tierra con Marte. Para ello restamos los vectores que unen ambos planetas con el centro de sus órbitas (en otras palabras, los vectores de posición de los planetas respecto al Sol). De está forma, si representamos la posición de dicho vector en cada instante de la órbita, podemos simular el movimiento relativo que vemos desde la Tierra.
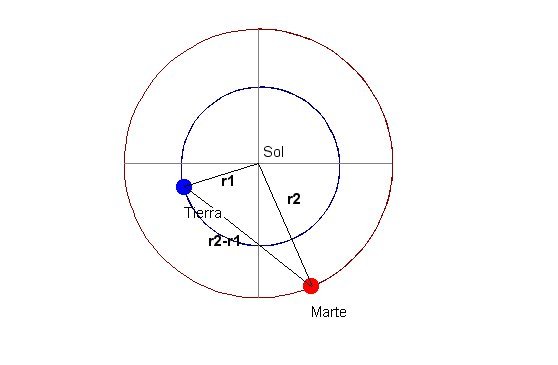
Para más información puede consultarse la siguiente página, donde se explica en profundidad el modelo ptolemaico. Las imágenes marcadas con un * han sido tomadas de dicho site.