A veces encontrar la solución analítica de una ecuación diferencial resulta muy complicado y muchas veces imposible, sin embargo prácticamente en todos los casos es posible encontrar valores de nuestra función en un conjunto discreto de puntos, eso lo conseguimos aproximando las derivadas por fracciones de incrementos de la función y de las variables, pasaremos así de una expresión diferencial a una algebraica.

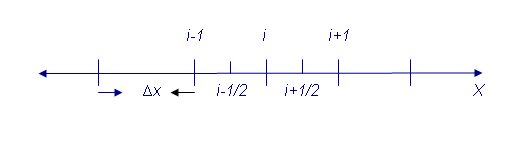
Supongamos que tenemos una función de x, f(x), para encontrar una expresión que nos discretice la derivada segunda de la función comenzaremos por dividir el eje X en un partes iguales de longitud Δ x como se muestra en la figura.

Sustituimos las derivadas por sus fracciones incrementales.

Esta será la expresión que tendremos que utilizar para convertir nuestra ecuación con derivadas segundas en una ecuación algebraica facilmente programable. Hay que tener muy presente que para conocer el valor de la función en un punto necesitamos conocer su valor en los dos anteriores.

Introducción al Cálculo Numérico >>  Discretización ecuaciones diferenciales >>  Discretización derivada segunda