1.- Introducción Teórica.

Una partícula que lleva una velocidad uniforme en un sistema de referencia inercial, y que por lo tanto su trayectoria es una recta, posee una trayectoria curvilínea si es observada desde un sistema de referencia que gira.

La partícula se mueve con velocidad uniforme en un sistema de referencia inercial, integrando la ecuación del movimiento, según se puede ver en la introducción al cálculo numérico: x_iner = x_iner + vx_iner*dt; y_iner = y_iner + vy_iner*dt; obtendremos una trayectoria recta.

Aplicamos la transformación de coordenadas de acuerdo con la relación entre las coordenadas de un punto respecto a dos ejes que están girados un ángulo w*t que viene dada por:

x_no_iner = x_iner*Math.cos(w*t) + y_iner*Math.sin(w*t);
y_no_iner = -x_iner*Math.sin(w*t) + y_iner*Math.cos(w*t);

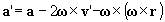
y observamos una trayectoria curvilínea, por lo que el observador que gira con el sistema de referencia detecta que la partícula tiene una aceleración para él, cuyo valor viene dado, de forma general, por la expresión: donde se ha indicado con primas las magnitudes medidas respecto al sistema que gira.

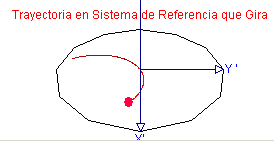
Asociando uno u otro conjunto de variables a una partícula observamos el resultado en la simulación.