

Imagen tomada de: http://www.kbglob.com/ciencia/un-avion-rompiendo-la-barrera-del-sonido/
| http://webs.um.es/jmz/optica/ | III. CAMPOS ELECTROMAGNÉTICOS |
Hasta ahora hemos hablado de ondas en una dimensión cuyo prototipo son las ondas que se propagan en una cuerda y cuyo ejemplo más notable son los instrumentos musicales de cuerda, en general las ondas se propagan en dos o tres dimensiones, en ejemplo muy típico de las primeras son las ondas en la superficie del agua y de las segundas las ondas sonoras y electromagnéticas, luz, radares, rayos X, TV, radio ….


Imagen tomada de:
http://www.kbglob.com/ciencia/un-avion-rompiendo-la-barrera-del-sonido/
A los puntos que tienen la misma amplitud se les denomina frente de ondas.
Un característica de todas las ondas es que su velocidad de propagación depende del medio en el que se propaga, ello da lugar a los fenómenos de reflexión y de refracción, este fenómeno es fácil de visualizar mediante el proceso geométrico propuesto por Huygens, astrónomo, físico y matemático holandés, nacido en La Haya en 1629, por el que cada punto al que llega una onda se convierte en emisor.
El modo de caracterizar la velocidad de propagación de las ondas electromagnéticas en un medio es mediante el llamado índice de refracción que se define como el cociente entre la velocidad de propagación en el vacío y la velocidad de propagación en el medio.
| c | velocídad en el vacío | |||
| n | = | —— | = | —————————— |
| v | velocídad en el medio |
En la imagen, tomada de una simulaciín de Walter Fendt, se muestra un frente plano que está incidiendo sobre una superficie plana que separa dos medios diferentes. Al llegar la onda a la superficie de separación de los dos medios cada elemento de esta superficie de separación se comporta como un emisor de ondas, la simulación nos permite llegar a la propagación de las ondas y su representación en frentes de onda o rayos, y visualizar los ángulos que forman los diferentes elementos involucrados.
Imagen tomada de la simulación: http://colos.inf.um.es/Cursos/Walter/phs/huygenspr_s.htm
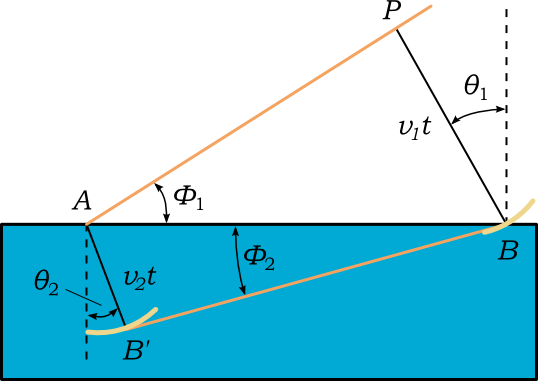 Esta situación la podemos esquematizar en la siguiente imagen.
En la imagen se dibuja el frente de ondas en el momento en que alcanza el segundo medio
en el punto A, al cabo de un tiempo t
el punto P ha recorrido v1*t mientras
que en el segundo medio en el mismo tiempo el frente ha recorrido v2*t.
Por relaciones trigonométricas podemos deducir de la imagen de la derecha.
Esta situación la podemos esquematizar en la siguiente imagen.
En la imagen se dibuja el frente de ondas en el momento en que alcanza el segundo medio
en el punto A, al cabo de un tiempo t
el punto P ha recorrido v1*t mientras
que en el segundo medio en el mismo tiempo el frente ha recorrido v2*t.
Por relaciones trigonométricas podemos deducir de la imagen de la derecha.
| v1*t | v2*t | sen θ1 | sen θ2 | |||||
| AB | = | ——— | = | ——— | ——→ | ——— | = | ——— |
| sen θ1 | sen θ2 | v1 | v2 |
Si multiplicamos ambos miembros por la velocidad de la luz c y a la relación entre esta velocidad y la velocidad de propagación de la onda en el medio la llamamos índice de refracción del medio, n, obtenemos la ley de Snell para la refracción.
| c | c | |||||||
| —— | sen θ1 | = | —— | sen θ2 | ——→ | n1* sen θ1 | = | n2* sen θ2 |
| v1 | v2 |
Al variar la velocidad con la que se propaga una onda la dirección del frente de ondas varía. Este hecho lo podemos utilizar para modificar la trayectoria de la luz en la forma que deseemos.
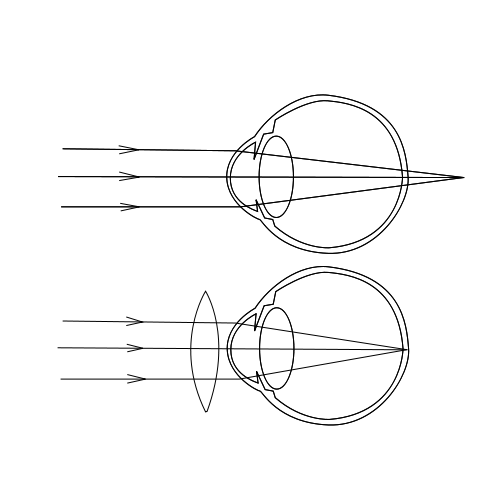
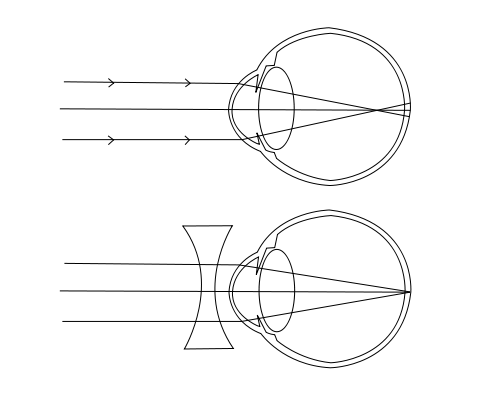
Las lentes nos permiten modificar las trayectorias de los rayos para que las imágenes se formen del mejor modo posible en la retina del ojo.
| José M. Zamarro. Universidad de Murcia | FUNDAMENTOS DE FÍSICA PARA ÓPTICOS |