I.2 Campos de fuerza: Gravitatorio, Electrostático
(ALGUNAS NOTAS SOBRE EL TEMA)
|
Vamos a introducir las interacciones gravitatoria y electrostática simultáneamente porque, como veremos, existen similitudes formales entre ambas. Las interacciones gravitatorias nos resultan más familiares que las eléctricas, por lo que el realizar un planteamiento paralelo nos hará más llevadera la introducción del campo eléctrico que resulta más abstracto.
I.2.a - Interacción gravitatoria
Comencemos con la interacción gravitatoria. Podemos proponer que los cuerpos en la superficie
de la Tierra son atraídos por ella, en la segunda mitad del siglo XVII Newton planteaba si estas
fuerzas son de la misma naturaleza que las que actúan entre los cuerpos celestes.
Comparando la caída de los cuerpos sobre la superficie de la Tierra con la caída de la Luna
hacia la Tierra propuso una ley de gravitación universal en la que se postula que las masas
de los cuerpos se atraen con una fuerza que es inversamente proporcional al cuadrado de sus distancias:
|
→
|
|
m1*m2
|
→
|
|
F
|
= G
|
—————
|
ur
|
|
|
|
d2
|
|
En la que m1 y m2 son las masas de los cuerpos que se suponen puntuales,
y d la distancia entre sus "centros". El vector fuerza tiene la dirección de la recta que une las masas y sentido de atracción entre ellas.
|

Imagen tomada de http://sol.sci.uop.edu/
Enlace caducado
|
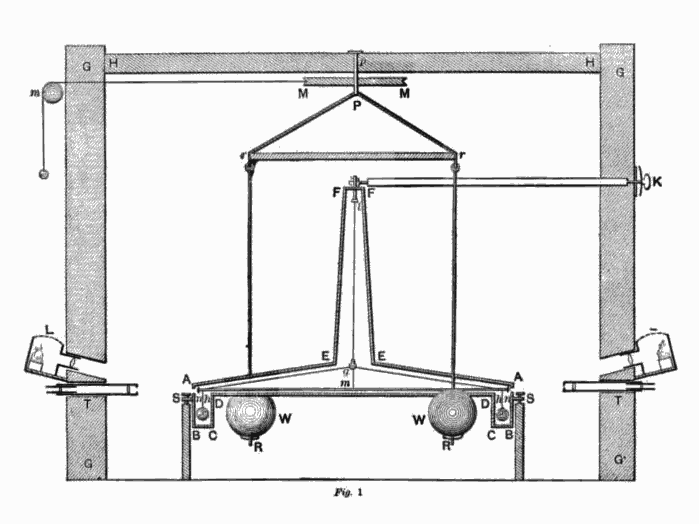
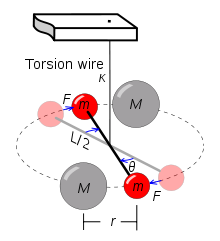
En 1789 Cavendish mide G utilizando una balanza de torsión
Imágenes tomadas de:
http://en.wikipedia.org/wiki/Cavendish_experiment
Esta expresión se conoce como "Ley de Gravitación Universal"
y hasta donde hoy sabemos todas las masas del universo interactúan siguiendo esta ley.
En 1789 Cavendish mide G convirtiéndose así
en el primer hombre que mide la masa de la Tierra.
La masa es una propiedad de las partículas elementales que forman la materia que conocemos,
que son los electrones y los quarks. Haciendo clic en la imagen se ejecuta una simulación
con la que se puede investigar la interacción entre dos masas.
Tarea I.2.1
a) Describe la experiencia
b) ¿Qué parámetros podemos modificar?
c) Planifica y ejecuta las experiencias posibles
d) ¿Qué podemos deducir?
e) Describe los resultados utilizando simbología matemática
|
Simulación tomada de:
http://phet.colorado.edu/en/simulation/gravity-force-lab
|
¿Porqué no hacemos esta experiencia en el laboratorio?
Tarea I.2.2
¿Porqué se atraen las masas?
Tarea I.2.3
¿Cómo se atraen las masas?
Para saber sobre cómo actúan las fuerzas sobre los cuerpos:
http://webs.um.es/jmz/www_movimiento/newton/newton.html
Tarea I.2.4
Teniendo en cuenta la ley de la dinámica de Newton y que la distancia a efectos gravitatorios
entre la Tierra y los objetos en su superficie se toma el radio de la Tierra
¿qué podemos hacer con la expresión de la ley de gravitacián universal?
a) Nada porque la ley de la gravitación universal sólo sirve para calcular las fuerzas entre los objetos celestes.
b) La ley de la dinámica de Newton, teniendo en cuenta la fuerza de atracción de la Tierra, nos permite obtener directamente la velocidad con que caen los objetos.
c) La ley de la dinámica de Newton, teniendo en cuenta la fuerza de atracción de la Tierra, nos permite obtener directamente la aceleración con que caen los objetos.
d) Aplicando la ley de la dinámica de Newton, a la fuerza con que la Tierra atrae a los cuerpos,
obtenemos que estos caen con una aceleración de 9.8 m/s2
I.2.a - Interacción Electrostática
Todos los cuerpos se encuentran formados por partículas que poseen carga eléctrica,
el hecho de que no percibamos habitualmente interacciones eléctricas, y sí gravitatorias,
siempre nos podemos caer, es debido a que en el caso de las masas todas se atraen, y en el caso
de las cargas hay de dos tipos, todos tenemos el mismo número de cargas de ambos tipos
por lo que sus efectos normalmente se anulan.
Podemos hacer experiencias en las que se muestra también que las interacciones entre las cargas vienen dadas por una expresión totalmente similar. La carga eléctrica es una propiedad de las partículas elementales que forman la materia que conocemos, que son los electrones y los quarks. Aunque las fuerzas eléctricas son comparativamente más fuertes que las gravitatorias, no podemos tomar una cantidad de carga y enfrentarla a otra con la facilidad con la que tomamos un kilogramo de hierro y lo enfrentamos a otro kilogramo. Coulomb (1736 - 1806) consiguió realizar esta experiencia utilizando una balanza similar a la de Cavendish
Si frotamos diferentes objetos podemos observar algunos efectos de interacción electrostática, se desprende de este hecho que las cargas tienen afinidades diferentes en diferentes materiales. En 1931 se le ocurrió al físico norteamericano Robert Van de Graaff construir una máquina en la que se optimizaba este fenómeno de electrificación por rozamiento.



Esta máquina se basa en una propiedad de los conductores, que no justificaremos, por la que si
una carga se encuentra en el interior de un conductor esta se mueve a su superficie. Mediante esta
máquina podemos conseguir una cantidad de carga razonable para realizar experiencias.
Vídeo cómo funciona el generador de Van de Graaff:
http://www.youtube.com/watch?v=I2G0IdTWGQU
La interacción entre cargas nos lleva a una expresión similar a la interacción
gravitatoria, la fuerza varía inversamente proporcional al cuadrado de la distancia entre las cargas.
Las expresiones para la interacción gravitatoria entre dos masas puntuales y la electrostática entre dos cargas puntuales son formalmente idénticas por lo que las propiedades básicas derivadas de las expresiones matemáticas también serán iguales, en ambos casos la fuerza disminuye con el cuadrado de la distancia y la fuerza tiene la dirección de la recta que une las partículas. El sentido de estas fuerzas difiere, en el caso de las masas estas siempre se atraen, en el caso de las cargas eléctricas nos encontramos con la necesidad de distinguir dos tipos de cargas al observar que las cargas que pertenecen a un grupo se repelen pero si son de distinto grupo se atraen.
|
→
|
|
q1*q2
|
→
|
|
|
F
|
= K
|
—————
|
ur
|
K = 1/(4 π ε0) = 8.99*109 N m2 C-2
|
|
|
|
d2
|
|
|
Donde a q1 y q2
las llamamos cargas eléctricas, la carga eléctrica es una propiedad de las partículas
elementales que forman la materia, que son los electrones y los quarks, en unidades internacionales
se mide en culombios, un culombio es la carga que situada a un metro de distancia de otra igual
interacciona con una fuerza de un newton, esta expresión es conocida como la ley de Coulomb
en honor a su descubridor.
¿Qué hace que en la naturaleza, y en la tecnología, las interacciones gravitatorias y las eléctricas intervengan de modo tan diferente? Tres son los principales factores que las diferencian:
-
Las cargas eléctricas pueden ser de dos tipos que denominamos como positivas y negativas, las del mismo signo se repelen mientras que de signos opuestos se atraen y en el universo existe la misma cantidad de carga de signo positivo como negativo, un cuerpo en general es neutro por lo que no apreciamos interacciones eléctricas entre ellos, mientras que todas las masas se atraen.
-
Otra diferencia se encuentra en la intensidad de las fuerzas, mucho mayor para las eléctricas para las mismas escalas.
-
Por último, si estudiamos situaciones en que se produzcan variaciones temporales los
comportamientos gravitatorios y eléctricos dejan de tener similitudes. Si se observan
las cargas en movimiento aparece una nueva interacción, la magnética, mientras que
la interacción entre las masas no varía, que nosotros sepamos apreciar, si estas se mueven.
El hecho de tener en cuenta variaciones temporales en los campos eléctricos y magnéticos
nos abre un mundo nuevo que nos llevará al electromagnetismo, a la luz.
Las fuerzas electrostáticas, comparadas con las gravitatorias son cuantitativamente menores, en las tareas II.1, II.2 y II.3 se pueden ver ejemplos en los que se puede apreciar qué entendemos por "cuantitativamente menores". A pesar de estas consideraciones sobre la intensidad de las fuerzas gravitatorias y eléctricas, en nuestro entorno en general prevalecen las interacciones gravitatorias frente a las eléctricas porque los cuerpos que nos rodean tienen el mismo número de cargas positivas como negativas y sus efectos se compensan mientras que las interacciones gravitatorias siempre se suman y su acción gobierna el movimiento del Sistema Solar, de nuestra Galaxia y del Universo.
Tarea I.2.5
¿Porqué predomina la fuerza gravitatoria frente a la eléctrica en las interacciones astronómicas?
Otro aspecto relevante es el comportamiento dinámico de las partículas elementales, estas partículas, que constituyen los átomos de los objetos que nos rodean y también nosotros mismos ¿se comportan como nuestro sistema solar? ¿podemos tratarlas con la mecánica newtoniana? Pensemos en dos moléculas de oxígeno de nuestra atmósfera, colisionan entre sí y con otras moléculas ¿se comportan las partículas que las forman como dos sistemas solares que colisionasen? Las estructuras atómicas que constituyen las moléculas son mucho más estables que los sistemas planetarios, su comportamiento ya no viene descrito por las leyes de Newton sino por la Mecánica Cuántica. El conocimiento del comportamiento de los electrones en estructuras sólidas compuestas por muchos átomos nos ha llevado a la utilización de conductores eléctricos hasta los chips de los ordenadores, teléfonos móviles… pasando por el transistor.
I.2.c - Campo: gravitatorio, electrostático
Una forma de describir estas interacciones es introduciendo el concepto de campo. Nosotros utilizaremos la palabra Campo, para hacer referencia a magnitudes que se encuentran definidas en cada punto del espacio, por ejemplo, campo de temperaturas, en todos los puntos del espacio podemos definir la temperatura en ese punto, campo gravitatorio, eléctrico…. En general no tiene sentido hablar de Campo sin ponerle ningún adjetivo.
Una masa es atraída con la misma fuerza por la Tierra siempre que se encuentre a la misma altura,
supongamos que es 1 Kg., y que nos encontramos en la superficie de la Tierra, la fuerza con que
la Tierra la atrae la llamamos Campo Gravitatorio en los puntos de la
superficie terrestre y la representamos por el vector:
Para calcular la fuerza que la Tierra ejerce sobre cualquier otra masa m en su superficie,
basta con multiplicarla por el valor del campo gravitatorio en ese punto:
En general el campo gravitatorio de una masa esférica como la Tierra en un punto alejado
d de su centro lo definimos como;
Tarea I.2.6
¿Cómo podemos detectar la existencia de campo gravitatorio en un punto?
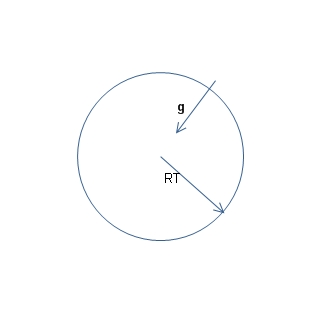
Tarea I.2.7
En la imagen se muestra la Tierra y el campo g que esta crea en su superficie.
a) Dibuja el campo en un punto situado a una altura igual al radio de la Tierra sobre esta
b) ¿Qué masa tendríamos que poner en ese punto para que la fuerza con que la Tierra lo atrae resulte igual a su peso en la superficie de la Tierra?
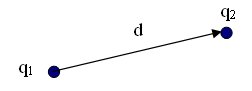
En el caso de la interacción electrostática la forma de definir campo eléctrico
es la siguiente, la fuerza que ejerce la carga uno sobre la carga dos la podemos expresar como:
|
→
|
|
q1
|
→
|
|
|
F
|
= k
|
———
|
ur
∗
q2
|
|
|
|
d 2
|
|
Si en lugar de q2 pusiéramos otra carga la expresión sería
la misma pero sustituyendo simplemente la parte final en la que aparece la carga, hay una
parte de la expresión que sólo depende de la carga uno y del punto del espacio
en el que se encuentre la otra carga, a esta parte la llamamos campo de la carga uno que crea
en el punto que se considere
con lo que la fuerza que ejerce la carga uno sobre la dos la podemos escribir como:
|
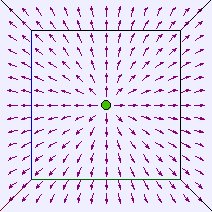
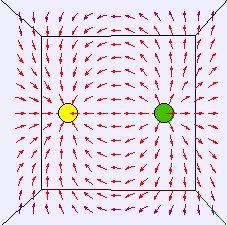
En la imagen se observa una representación de la dirección y sentido del campo en una retícula
de puntos para una carga y para dos cargas de signos opuestos. Al hacer clic sobre las figuras
se ejecuta un applet interactivo para mejorar la visualización de los campos.
|
|
Tarea I.2.8
¿Cómo podemos detectar la existencia de campo eléctrico en un punto?
 I.2.e - Líneas de Campo
I.2.e - Líneas de Campo
Líneas tangentes en cada punto al campo, las líneas del campo nacen en las cargas positivas y terminan en las negativas, una flecha indica hacia las cargas negativas. Cuando en una imagen veamos líneas de campo que no tienen principio o fin en dicha imagen en algún lugar debe haber cargas positivas en donde comiencen o cargas negativas en donde terminen. El campo de una carga puntual es radial, el campo de dos cargas depende de si las dos son de igual signo o de signos opuestos.
Podemos ver algunas distribuciones de cargas y la representación de sus campos en:
http://colos.inf.um.es/fislets/II4Electromagnetismo/II19CampoElectrico/il19_3.html
Campo eléctrico de dos cargas por Sadahisa Kamikawa





 Tarea I.2.7
Tarea I.2.7


