En la siguiente simulación podemos familiarizarnos con la expresión de la segunda ley de Newton, aplicándola a dos objetos con igual velocidad inicial. Trata de realizar la siguiente tarea comprobando con la simulación tus afirmaciones.

Tarea 02.3.2. Fuerza y movimiento Comenta los siguientes enunciados: a) Si la fuerza neta que se ejerce sobre un cuerpo es en la misma dirección y sentido que la velocidad que lleva ese cuerpo, su velocidad aumenta. b) Si la fuerza neta que se ejerce sobre un cuerpo es en la misma dirección, pero sentido opuesto, que la velocidad que lleva ese cuerpo, su velocidad aumenta. c) Si la fuerza neta que se ejerce sobre un cuerpo tiene dirección perpendicular a la velocidad que lleva ese cuerpo su velocidad aumenta. d) Si la fuerza neta que se ejerce sobre un cuerpo tiene dirección perpendicular a la velocidad que lleva ese cuerpo, su velocidad no aumenta pero varía su dirección.

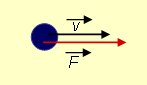
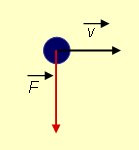
En la siguiente simulación encontramos dos cuerpos iguales, una bola, que tienen la misma velocidad inicial y la misma fuerza aplicada salvo la dirección en la que está aplicada. En el primer cuerpo la fuerza está aplicada en la misma dirección y sentido que la velocidad, mientras que en el siguiente cuerpo, bola roja, la fuerza está siempre actuando perpendicularmente a la velocidad.

Inicialmente la simulación nos muestra las velocidades de los dos cuerpos, que son iguales en módulo dirección y sentido. Si activamos la simulacón la velocidad del objeto superior aumenta mientras que el valor de la velocidad del otro cuerpo permanece constante pero su dirección varía. Si seleccionamos "VER F" observamos las fuerzas que actúan.

Si seleccionamos “Variación velocidad” podemos observar cómo podemos obtener la variación de velocidad en el caso de un movimiento circular.

Tarea 02.3.3. Fuerza y movimiento
Dos partículas con la misma masa y velocidad inicial, al cabo de un cierto tiempo muestran la situación que se muestra en la imagen, comentar cual de las siguientes afirmaciones es más adecuada.

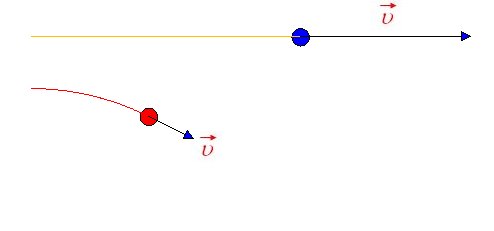
a) Sobre ambas partículas actúa una fuerza que puede tener el mismo módulo en ambos casos pero cuya dirección y sentido en la primera partícula es igual que la velocidad inicial, mientras que en la segunda es perpendicular.
b) Sobre la primera partícula no actúa ninguna fuerza.
c) Sobre la primera partícula actúa una fuerza mayor que sobre la segunda.
d) Sobre ambas partículas actúa una fuerza que es mayor en la primera partícula y su dirección y sentido es igual que la velocidad inicial, mientras que en la segunda es perpendicular.

Las ecuaciones diferenciales tienen la genial propiedad de tener infinitas soluciones por lo que, según el problema que estudiemos, podemos estar en el caso de un objeto que se nos cae de las manos o en una piedra que lanzamos, lo que nos dará una u otra solución serán las condiciones iniciales, es decir, la posición y velocidad iniciales.

¿Porqué en Física nos aparecen tantas ecuaciones diferenciales?
El objetivo de la Física es describir la naturaleza, observamos que en esta la variación es un elemento esencial, variaciones espaciales, variaciones temporales, el operador matem´tico derivada es equivalente a variación, por eso utilizamos las derivadazas en Física y por lo tanto lo que denominamos ecuaciones diferenciales. Recordemos la definición de derivada: