| http://webs.um.es/jmz/optica/ | II - ONDAS |
II.5.1 - Mecanismo de propagación de una onda en una cuerda tensa.
II.5.2 - Apliquemos nuestros modelos matemáticos.
II.5.3 - Velocidad de propagación en cuerdas
Dividimos la cuerda en segmento y nos fijamos en uno de ellos que marcamos en rojo.

Para que una cierta masa modifique su velocidad hace falta que sobre ella actúe una fuerza.
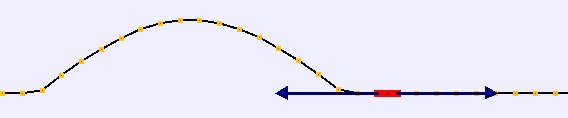
Si se encuentra un pulso viajando por la cuerda tensa, antes de que llegue este al elemento de cuerda actúan dos fuerzas de igual valor y dirección pero de sentidos opuesto, la tensión. El elemento de cuerda se encuentra en reposo y la resultante de las fuerzas que actúan sobre el es cero por lo que continúa en reposo.

El pulso es una deformación de la posición de los elementos de la cuerda respecto de su posición de equilibrio, ahora las fuerzas que actúan sobre el elemento continúan siendo de igual valor pero las direcciones han cambiado por lo que la resultante ya no es nula. En la imagen se ha dibujado únicamente la componente vertical de la resultante, que es la que nos interesa para estudiar el desplazamiento del elemento de cuerda.
Podemos trabajar este aspecto con la simulación:
En una cuerda tensa un pequeño trozo de la misma se encuentra sometido a dos fuerzas de igual valor pero de sentidos opuestos, la tensión de la cuerda, cuando llega una perturbación la dirección de las fuerzas cambia de modo que aparece una componente vertical que comunica una cierta aceleración al elemento de cuerda. Como siempre que queremos estudiar un movimiento utilizaremos la 2a ley de Newton para estudiar el movimiento del elemento de cuerda.
Como siempre que queremos estudiar un movimiento utilizaremos la 2a ley de Newton para estudiar el movimiento del elemento de cuerda.
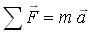
En nuestro caso estudiamos el desplazamiento vertical del elemento de cuerda por lo que solamente trabajaremos con la componente y de esta ecuación.

El movimiento vertical de cualquier elemento infinitesimal esta originado por la fuerza resultante de las tensiones en ambos extremos, en una aproximación para pequeños desplazamientos. Esta fuerza tiene por tanto solo componente vertical y para estudiar el fenómeno debemos plantear que su valor es igual a la masa por la aceleración en el elemento considerado.
La figura permite amplificar una situación para analizar las fuerzas que actúan en cierto instante sobre un elemento de longitud infinitesimal. Supongamos éste comprendido entre las abcisas x y x + Δx
El valor de su desplazamiento viene dado por la coordenada vertical y, por consideraciones geométricas, se obtiene que la fuerza vertical es
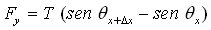
Para ángulos pequeños podemos sustituir el seno por la tangente, luego se verá porqué hacemos este cambio.
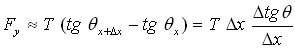
En donde hemos multiplicado y dividido por Δx. Esta es la fuerza que produce las variaciones de velocidad del elemento de cuerda que estamos estudiando. Antes de utilizarla en la ecuación de Newton juguemos con ella, este juego resulta un poco farragoso y hasta trabalenguas por lo que posiblemente requiera de varias lecturas cuidadosas
Si utilizamos el concepto de derivada como límite de un cociente de incrementos podremos escribir:
| Δ tg θ | ∂ tg θ | |
| --------- | ⇒ | --------- |
| Δ x | ∂ x |
Donde suponemos que Δx es tan pequeño como queramos.
Vayamos ahora con la relación que existe entre la tangente y la interpretación gráfica de la derivada. “La tangente del ángulo que forma la tangente a una curva resulta coincidir con el valor de la derivada de la función en ese punto” .
Revisar el final del apartado 3 del capítulo II: - Las leyes del movimiento de Newton.
Ver interpretación gráfica de la derivada en:
http://www.catedu.es/matematicas_blecua/bacmat/temario/bac1/mat1_09derivada.htm
| ∂ y | |
| tg θ = | ------ |
| ∂ x |
sustituimos el valor de la tangente en la anterior expresión:
| ∂ | ∂ ∂ y |
| ----- tg θ = | ----- ----- |
| ∂ x | ∂ x ∂ x |
obtenemos que esa fuerza la podemos escribir como:
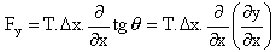
Puesto que la interpretación geométrica de la derivada iguala su valor en un punto con la tangente del ángulo que forma la tangente a la curva en ese punto. Suponiendo que la cuerda posee una masa por unidad de longitud μ, la masa del elemento bajo estudio es μ∗Δ x,
Considerando la aceleración como derivada segunda del desplazamiento respecto al tiempo, la aplicación de la 2a ley de Newton nos lleva a escribir la ecuación de movimiento como:
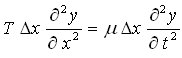
Simplificando obtenemos que el desplazamiento de cualquier punto de la cuerda cumple una ecuación de la forma:
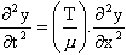
A este modelo de ecuación lineal (debido a que la función y sus derivadas se presentan solo en primera potencia) deducida para ángulos pequeños, le llamamos ECUACIÓN DE ONDAS y sus soluciones particulares nos dan expresiones de la FUNCIÓN DE ONDA.
La magnitud física que corresponde a la función de onda en el caso de cuerdas es el desplazamiento vertical y. En la ecuación de onda vemos que la aceleración de un elemento ∂2y/∂t2, está relacionada con el grado de curvatura de la cuerda ∂2y/∂x2.
Comparando esta expresión con la general obtenida previamente para todas las ondas concluimos que la velocidad de propagación de una perturbación en una cuerda tensa viene dada por:
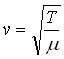
Es un resultado bastante razonable:
Vemos cómo la velocidad de propagación de una onda en una cuerda depende de características de la misma, ese hecho es extensible a otros medios: la velocidad de propagación de una onda en un medio depende de las características de dicho medio .
| José M. Zamarro. Universidad de Murcia | FUNDAMENTOS DE FÍSICA PARA ÓPTICOS |