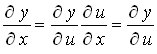
| http://webs.um.es/jmz/optica/ | II - ONDAS |
El poder de las matemáticas: Del concepto de ONDA a la LUZ
Juguemos un poco con las matemáticas, es el mejor modo de aprender. Sabemos que la expresión matemática que nos represente una onda que se propaga hacia la derecha del eje x con velocidad v, debe ser una función que dependa del espacio y del tiempo, esto lo podíamos expresar en una dimensión:
Derivemos dos veces respecto a x y derivemos también dos veces respecto a t y comparemos estos resultados. Para ello llamaremos u a x - vt y practicamos la regla de calcular lo que varía una función respecto de una variable de la que no depende directamente, concretamente f depende de x a través de u.
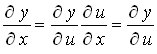
puesto que la derivada de u respecto a x es uno, si volvemos a derivar respecto a x simplemente obtendremos la derivada segunda respecto a u
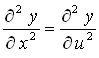
Calculemos ahora la variación respecto a t.
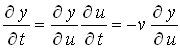
puesto que la derivada de u respecto a x es - v, si volvemos a derivar respecto a t es lo mismo que derivar respecto a u y multiplicar por - v.
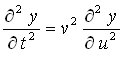
Comparando ambas expresiones llegamos a la conclusión de que si una función matemática representa una onda, derivando dicha expresión dos veces respecto al espacio y dos veces respecto al tiempo nos va a dar la misma función salvo un factor que resulta ser la velocidad de propagación de la onda al cuadrado
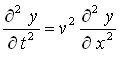 3.1
3.1
 Seguro que ha resultado algo duro este proceso matemático pero esperemos que el resultado compense el esfuerzo.
En este tipo de expresiones nace algo que probablemente hoy nos resulte “casi” imprescindible, el móvil,
a mediados del siglo XIX un físico matemático de nombre roquero Maxwell, encontró una expresión similar
pero con el campo eléctrico como magnitud que se propagaba y su sorpresa fue que encontró
que el valor que obtenía para v era del orden de 300 000 km/s
¡una razón más
que justificada para afirmar que la luz era una onda electromagnética!
Se había abierto la veda para el mundo de las comunicaciones.
Seguro que ha resultado algo duro este proceso matemático pero esperemos que el resultado compense el esfuerzo.
En este tipo de expresiones nace algo que probablemente hoy nos resulte “casi” imprescindible, el móvil,
a mediados del siglo XIX un físico matemático de nombre roquero Maxwell, encontró una expresión similar
pero con el campo eléctrico como magnitud que se propagaba y su sorpresa fue que encontró
que el valor que obtenía para v era del orden de 300 000 km/s
¡una razón más
que justificada para afirmar que la luz era una onda electromagnética!
Se había abierto la veda para el mundo de las comunicaciones.
1.-- Onda: Perturbación que se propaga y = f(x, t)
2.-- Acompañando a la onda y = f(x - v*t)
3.-- Las variaciones de esta función respecto al espacio y respecto al tiempo son iguales salvo un factor que está relacionado con la velocidad de propagación de la onda.
4.-- Maxwell, jugando con las ecuaciones que cumplen los campos eléctricos y magnéticos, encuentra una ecuación similar:
 5.-- El factor que le aparece relacionando las variaciones espaciales y temporales de los
campos vale 300 000 km/s, la velocidad con la que se propaga la luz.
5.-- El factor que le aparece relacionando las variaciones espaciales y temporales de los
campos vale 300 000 km/s, la velocidad con la que se propaga la luz.
| José M. Zamarro. Universidad de Murcia | FUNDAMENTOS DE FÍSICA PARA ÓPTICOS |