wxMaxima

Palabras clave: wxMaxima

1. Introducción

Maxima es un sistema para la manipulación de expresiones simbólicas y numéricas, incluyendo diferenciación, integración, expansión en series de Taylor, transformadas de Laplace, ecuaciones diferenciales ordinarias, sistemas de ecuaciones lineales, vectores, matrices y tensores. Maxima produce resultados de alta precisión usando fracciones exactas, números enteros de precisión arbitraria y números de coma flotante con precisión variable. Adicionalmente puede graficar funciones y datos en dos y tres dimensiones

— Página oficial de Maxima

wxMaxima is a document based interface for the computer algebra system Maxima. wxMaxima provides menus and dialogs for many common maxima commands, autocompletion, inline plots and simple animations. wxMaxima is distributed under the GPL license.

— Página oficial de wxMaxima

wxMaxima puede descargarse en la dirección http://andrejv.github.io/wxmaxima/

2. Cómo funciona

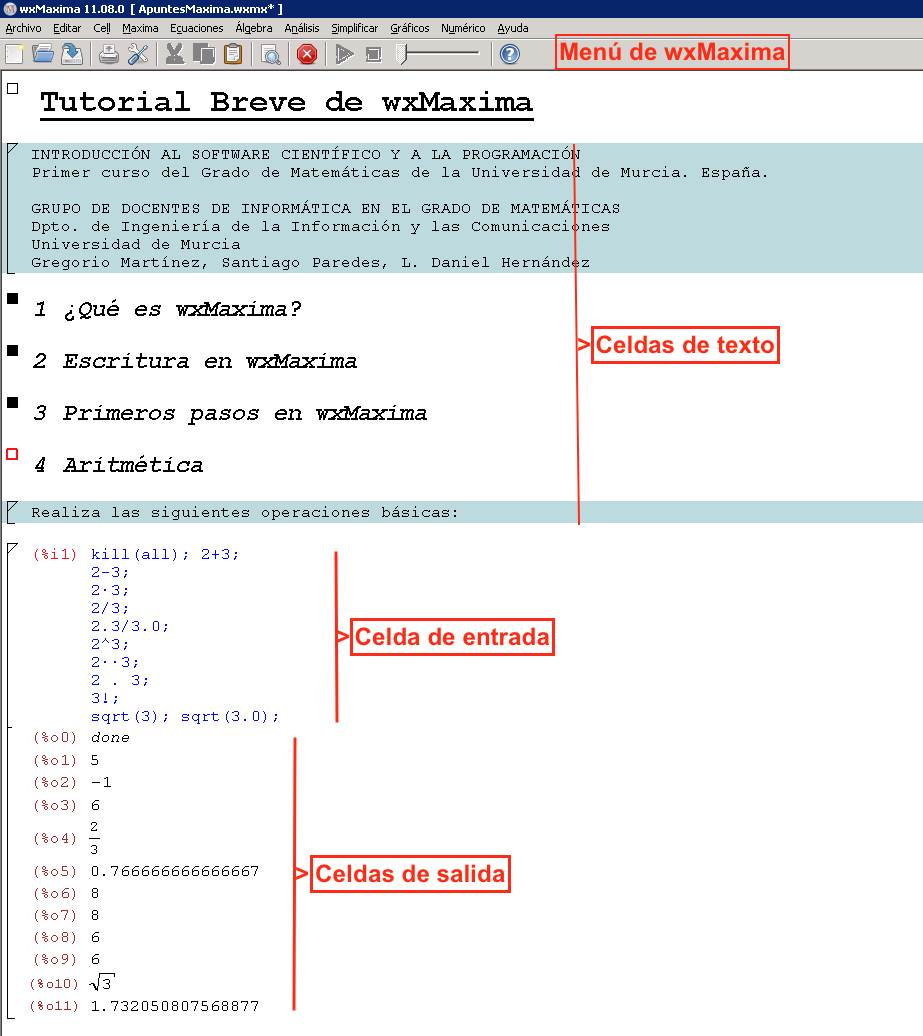
En wxMaxima se pueden crear varios tipos de celdas: de texto, de entrada y de salida.

En las de texto puedes escribir los contenidos que desees, incluso en LaTeX.
En las celdas de entrada debes de introducir una o varias instrucciones de wxMaxima.
En las celdas de salida se muestran los resultados de las celdas de entrada. Para generar un resultado debes activar una celda de entrada y pulsar SHIFT-ENTER para evaluar las expresiones.

Así pues, lo único que te queda es conocer instrucciones/funciones de wxMaxima.

3. Algunas instrucciones

No vamos a dar una lista exhustiva de instrucciones pero sí se muestran algunas para que veas la potencia que tiene wxMaxima:

Instrucciones Acciones

Instrucciones	Acciones
1+1;	Suma 1 y 1.
sqrt(2 * %pi);	Calcula la raíz cuadrada de 2 por el número PI
radio: 10 $ altura: 100 $ area: %pi * radio^2; volumen: area * altura;	Asigna valores a las variables `radio` y `altura` para calcular un volumen ¿de qué figura?
integrate( sin(x), x);	Calcula la integral indefinida de la función `sen(x)`.
integrate( sin(x), x, 0, %pi);	Calcula la integral definida de la función `sen(x)` en el intervalo [0,PI].
f(x) := x^2 + a$ f(5); f(5), a = -5;	Define una función `f(x)`. La instrucción `f(5)` dará como resultado `25+a`. La instrucción `f(5), a = -5;` dará como resultado el valor `20`.
A: matrix([1,-1], [1,sin(c)]); B: invert(A);	Define una matriz `A` y define una matriz `B` como la inversa de `A`.
f(x) := x^2 $ diff(f(x), x); g(y) := sin(y)$ g(f(x)); diff( g(f(x)) , x);	Define una función `f(x)` y calcula su derivada. A continuación define una función `g(y)` y calcula la composición de `f` con `g` y la derivada de dicha composición.

1+1;

Suma 1 y 1.

sqrt(2 * %pi);

Calcula la raíz cuadrada de 2 por el número PI

radio: 10 $
altura: 100 $
area: %pi * radio^2;
volumen: area * altura;

Asigna valores a las variables radio y altura para calcular un volumen ¿de qué figura?

integrate( sin(x), x);

Calcula la integral indefinida de la función sen(x).

integrate( sin(x), x, 0, %pi);

Calcula la integral definida de la función sen(x) en el intervalo [0,PI].

f(x) := x^2 + a$
f(5);
f(5), a = -5;

Define una función f(x). La instrucción f(5) dará como resultado 25+a. La instrucción f(5), a = -5; dará como resultado el valor 20.

A: matrix([1,-1],
        [1,sin(c)]);
B: invert(A);

Define una matriz A y define una matriz B como la inversa de A.

f(x) := x^2 $
diff(f(x), x);
g(y) := sin(y)$
g(f(x));
diff( g(f(x)) , x);

Define una función f(x) y calcula su derivada. A continuación define una función g(y) y calcula la composición de f con g y la derivada de dicha composición.