Palabras clave: Datos estructurados, Arrays.
1. Concepto de array
Son arrays las listas de valores del mismo tipo, ya sean de tipo de dato simple o tipo de dato estructurado.
| Un array recolecta varios datos y todos los datos tienen que ser del mismo tipo. |
Cada uno de los valores del array es accesible mediante un índice. Los valores del índice se denomina rango y toma valores entre 0 y length-1, siendo length el número de valores que almacena el array.
2. Declaración de una variable de tipo array
Un array se declara en Processing como:
TipoDeDato[] variable;
Imagina que se quiere almacenar los primeros términos de una sucesión aritmética.
Cada elemeno de la sucesión será un natural (entero), por lo que usar el tipo de dato array estaría justificado.
Podríamos entonces declarar la variable sucesión como:
1 int[] sucesión;
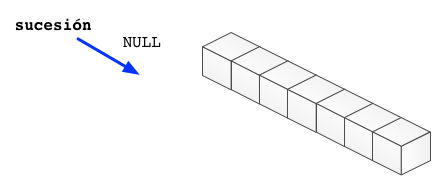
Cuando declaramos una variable de tipo referencia (como es el tipo array), dicha variable toma el valor NULL para indicar que no sabe a qué parte de la memoria (Heap) tiene que referenciar para recuperar o guardar datos. |
|
3. Inicialización de arrays
Cuando declaras una variable de "tipo array", la variable está preparada para almacenar una referencia al lugar de la memoria donde se almacenarán los valores (todos del mismo tipo).
| Cuando se trabaja con estructuras de datos siempre se tiene que reservar de forma explícita la memoria necesaria para almacenar todos los datos que guardará el tipo de dato estructurado. |
Siempre hemos de usar la instrucción new para que se reserve una porción de memoria para cada uno de los valores que se almacenarán en el array, y se le asigne una referencia a la variable "que apunte" a ese conjunto de valores.
La sintaxis general es:
variable = new TipoDeDato[n]; // Observa los corchetes []
El TipoDeDato debe de coincidir con el tipo de dato con el que declarastes la variable variable.
El valor de n debes sustituirlo por el número de valores que quieras recolectar en la variable variable.
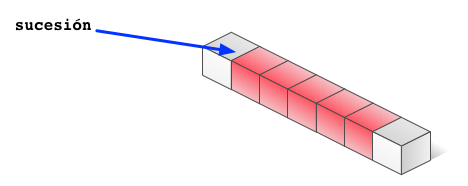
Continuando con el ejemplo anterior, para inicializar la variable sucesión,
escribiremos la instrucción:
1 sucesion = new int[5];
Cuando usamos la instrucción |
|
Con arrays no olvides añadir los corchetes con el número de valores a guardar cuando uses la instrucción new.
|
Otra forma de interpretar la acción variable = new int[n] es como la creación
de n-variables de tipo entero.
|
4. Acceso a los valores de un array
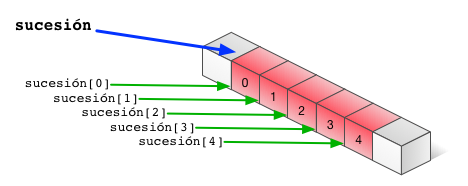
Si se declara una variable como una estructura array que almacenará n valores,
para acceder a dichos valores se usan las expresiones:
variable[0] variable[1] ... variable[n-1]
El acceso a la posición (i+1)-ésima del array se expresa como variable[i].
El símbolo i recibe el nombre de índice del array y toma valores entre 0 y n-1, siendo n el número de valores almacenados.
Si el índice de un array toma valores negativos o superiores a n-1 obtendrás un mensaje en tiempo de ejecución.
|
En Processing, cuando usas un índice fuera de rango obtendrás este mensaje de error: siendo k el valor del índice que está fuera del rango. |
No confundas el índice i (que hace referencia a una posición) con el valor almacenado en dicha posición variable[i], que recibe el nombre de término.
| No confundas el índice con el término asociado a ese índice. |
Si se interpreta int[] variable como un conjunto de variables,
la expresión variable[i] se corresponde con el nombre de la i-ésima variable.
Es decir, se disponen de las siguientes variables de tipo int: variable\(_0\), variable\(_1\), variable\(_2\), …
|
Continuando con el ejemplo anterior del array de 5 enteros.
Mientras que |
|
4.1. Conocer el número de elementos que tiene un array
Si sobre un array se da la instrucción:
variable = new TipoDeDato[n];
se trabajará con una estructura que almacenará n valores, el número n recibe el nombre de tamaño o longitud del array.
Si queremos acceder a todos y cada uno de los elementos de un array necesitaremos conocer cuál es el tamaño del array. Si es conocido, podemos utilizar una variable-índice que tome valores en todo su rango y así poder acceder a todos los términos. Pero ¿cómo sé sabe la longitud de un array? ¿se necesita una variable para cada array que almacene el tamaño de dicho array? No siempre es necesario. En la gran mayoría de los lenguajes de programación existen variables o procedimientos que permiten calcular el tamaño de un array.
En Processing, para conocer el número de elementos que tiene un array se usa la expresión variable.length.
|
|
Otra forma de acceder a todos los valores de un array es mediante las expresiones: variable[0] variable[1] ... variable[variable.length-1] |
4.2. Asignación de valores a un array
Recuerda que la asignación de un valor a una variable simple es mediante la instrucción:
variable = valor;
Si variable es un array, entoces representa a un conjunto de variables \(\{ \) variable[i]\( | i=0,..,n-1\}\). Así, la asignación de un valor a cada una de esas variable simples será mediante las instrucciones:
variable[0] = valor0; variable[1] = valor1; ... variable[variable.length-1] = valorK;
La estructura secuencial anterior almacena en cada término un valor. Una estructura secuencial no es factible para asignar valores a todos los términos y más cuando el tamaño del array puede ser grande. Para solventar el problema se recurre a una estructura repetitiva como la siguiente:
for (int i=0; i<variable.length; i++) {
acciones sobre variable[i]
}
Empezamos realizando una acción sobre el elemento variable[0], y en cada iteración operamos sobre el elemento variable[i], y finalizamos con el elemento variable[variable.length-1]. La acción puede ser cualquiera que consideres, por ejemplo, una asignación.
Hay casos en los que viene bien interpretar variable[i] como el término i-ésimo de una lista.
Pero en muchos otros casos es mejor interpretar variable como un conjunto de variables y
considerar variable[i] como la i-ésima variable. Usa la interpretación que mejor consideres para tu problema.
|
Continuando con el ejemplo anterior, podemos asignar valores a la variable sucesion de la siguiente forma:
1
2
3 for (int i=0; i<variable.length; i++) {
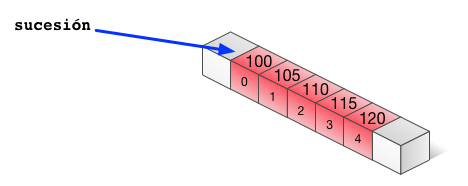
sucesion[i] = 100 + i*5;
}
con ello generamos la sucesión \(\{100, 105, 110, 115, 120\}\); la sucesión aritmética de 5 términos, que empieza en el 100 y con diferencia 5. |
|
|
Cuando se conocen los elementos exactos que tendrá un array se puede realizar la reserva de memoria y asignación en una única instrucción: TipoDeDato[] variable = {dato1, dato2, ..., datoN};
|
4.3. Recuperación de valores de un array
Si la recuperación del dato almacenado en un variable se consigue mencionando a la variable, en un variable de tipo array bastará mencionar o acceder al término asociado a un índice concreto.
| Mencionar a la variable de tipo array no recupera todos los datos asociados al array. Recuerda que una variable de tipo array almacena una referencia al lugar de la memoria donde se encuentran la lista de valores asociada a la variable. |
|
Continuando con el ejemplo anterior, para imprimir los valores del array sucesión
basta recorrer todas las posiciones y recuperar el término asociado:
1
2
3 for (int i=0; i<variable.length; i++) {
println("Término " + i + ":" + sucesion[i]);
}
5. Arrays y funciones
-
Si en una función un parámetro responde a un array, puedes usarlo como una vía de entrada de datos a la función, pero también nos sirve para retornar datos de salida.
-
Si este es tu propósito, nunca apliques un
newsobre el parámetro, pues perderás la referencia original. -
No olvides nunca que si tienes aliasing sobre el argumento de una función, la modificación de los valores asociados a este argumento también modificará a la otra variable.
-
-
Si en una función quieres retornar un tipo de dato array tendrás que
-
declarar una variable local,
var, del tipo array, -
reservar la memoria correspondiente para dicha variable,
var = new TipoDato[n];, -
asignar el conjunto de valores a la variable mediante
var[indice], -
retornar el conjunto de valores con
return var;
-
Mediante el uso de arrays queremos hacer un programa que:
-
determine si dos rectas generadas aleatoriamente, con coeficientes no nulos, son secantes o no.
-
modique los parámetros de una recta para obtener una recta paralela a ella y use la función construida para retornar la pendiente de dicha recta.
Para ello consideramos los siguientes resultados.
-
Dadas dos rectas, \(r\equiv Ax+By+C=0\) y \(s\equiv A'x+B'y+C'=0\), las dos rectas son secantes (se cortan en un punto) sii \(\frac{A}{A'}\not = \frac{B}{B'}\). En otro caso son o paralelas o son la misma.
-
Dada una recta \(r\equiv Ax+By+C=0\) se puede calcular su pendiente a partir de la expresión \(-\frac{A}{B}\).
Comenzamos estableciendo cómo vamos a representar una recta mediante un array.
La expresión de una recta se puede presentar en forma vectorial, paramétrica, continua, etc.
En los resultados matemáticos nos dan las expresiones en forma general, y esta es la forma en la
que vamos a suponer que nos vienen dadas todas las rectas.
En la forma general \(Ax+By+C=0\) se requiere de una lista de 3 valores reales, \(\{A,B,C\}\), para caracterizar a cualquier recta y como tal lista, y a además del mismo tipo de valor (real), puede
ser modelada o representada mediante un array de 3 elementos.
Es decir, supondremos que una variable con nombre recta representa una recta si queda declarada como
float[] recta;
Para poder utilizar un variable de tipo float[] como algo que codifique una recta deberemos de hacer una reserva de memoria para 3 números reales.
Es decir, antes de cualquier operación sobre dicha variable se deberá de ejecutar la instrucción:
recta = new float[3];
Así declarado y definido, usaremos el término 0 para guardar el coeficiente \(A\), el término 1 para guardar el coeficiente \(B\) y el término 2 para guardar el coeficiente \(C\).
Con este acuerdo en la codificación de la información disponible de una recta, definimos la siguiente función como la encargada de crear rectas aleatorias:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 /**
* Función generadora de rectas aleatorias
* @return, Una nueva recta (codificada como array)
*/
float[] generaRecta() {
float[] aux; // Declaramos una variable para almacenar una lista
aux = new float[3]; // Reservamos memoria y guardamos la referencia
// Asignamos valores aleatorios a cada término
for (int i=0; i<aux.length; i++) {
aux[i] = 0;
while (aux[i] == 0) { // Tienen que ser valores no nulos
aux[i] = random(-1000, 1000); // negativos o positivos.
}
}
return aux; // Retornamos la referencia del nuevo array
}
Esta función la utilizaremos en la función principal para crear dos rectas como puedes ver en el siguiente código:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 /**
* Función principal
*/
void setup() {
// Declaramos dos rectas
float[] r, s;
// Generamos dos rectas aleatorias
r = generaRecta();
s = generaRecta();
if (sonSecantes(r, s))
println("Son rectas secantes");
else
println("NO son rectas secantes");
}
La función principal no solo crea dos rectas. También invoca a una función para comprobar si las dos rectas son secantes o no. Dicha función se define como sigue:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 /**
* Función que comprueba si dos rectas son secantes
* Hay que comprobar si \frac{A}{A'}\not = \frac{B}{B'}
* Se asume la ecuación de la forma Ax+By+C=0
* @param r1, una recta
* @param r2, la otra recta
* @return, true si son paralelos y false en otro caso
*/
boolean sonSecantes(float[] r1, float[] r2) {
float cocienteA = r1[0]/r2[0]; // El primer término, coeficiente de x, es r[0]
float cocienteB = r1[1]/r2[1]; // El segundo término, coeficiente de y, es r[1]
if (cocienteA != cocienteB) return true;
else return false;
}
Con esto concluimos la primera parte del ejercicio. Para la segunda parte, se nos pide una función que modique los parámetros de una recta para obtener una recta paralela a ella y que se use dicha función para retornar la pendiente de dicha recta.
Como se trata de modificar una recta dada, diseñaremos una función que contemple como parámetro un array que se utilizará como via de entrada y salida de datos. Además la función debe retornar un número real, la pendiente de dicha recta. En concreto definimos esta función:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 /**
* Modifica una recta para obtener una recta paralela a una dada.
* También retornamos la pendiente de la recta.
* La pendiente de Ax+By+C=0 es -A/B.
* @param recta, la recta de entrada (y de salida)
* @return la pendiente de la recta
*/
float pendienteParalela(float[] recta) {
// Calculamos un número aleatorio que será el que
// multiplique a todos los coeficientes de la recta
float factor = random(1, 200); // El factor
// Asignamos nuevos valores a cada coeficiente
for (int i=0; i<recta.length; i++)
recta[i] = recta[i] * factor;
// Retornamos la pendiente
return -recta[0]/recta[1];
}
que será invocada en el programa principal como:
1
2
3
4 // Modifica r, para obtener una recta paralela a ella
// y calculamos su pendiente
print("La pendiente es: ");
println(pendienteParalela(r));
6. Repaso
-
Un array es una estructura formada por una lista de valores, todos del mismo tipo.
-
Antes de usar una variable de tipo array siempre hay que usar la instrucción
new TiposDato[n], siendonel número de elementos que contendrá la lista. -
Para acceder a un valor se usa un índice:
nombreVariable[indice]. -
variable[i]se puede interpretar como el i-ésimo elemento de una lista o como la variable i-ésima de un conjunto de variables. -
Si usas un array como parámetro en una función lo puedes usar para suministrar datos de entrada o para modificar valores del argumento.
-
Si una función retornara un array, deberás de declarar una variable de tipo array, reservar memoria, asignar valores a los términos y aplicar
returna dicha variable.