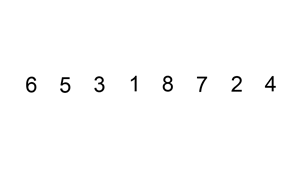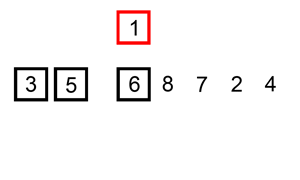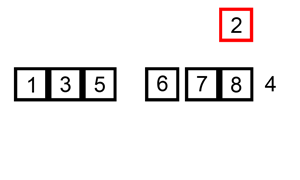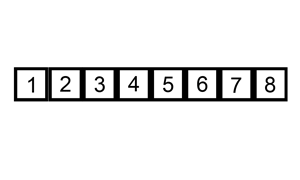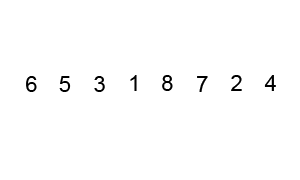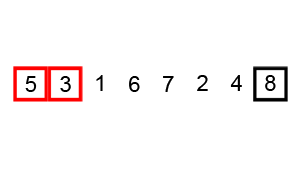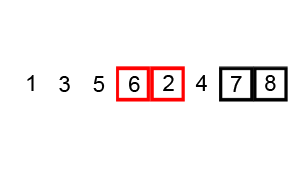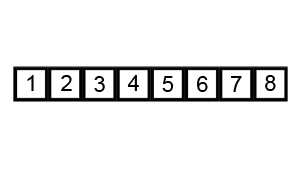Algoritmos básicos sobre conjuntos de datos

Palabras clave: Algoritmos, Búsqueda, Ordenación.

Preguntas de repaso

¿Cómo se inicializa la memoria para un array escalonado?
¿Cómo se inicializa la memoria necesaria para trabajar con una matriz de registros?

No sigas si no conoces las respuestas.

1. Motivación

Cuando se trabajan con conjuntos de datos aparecen muchas veces la misma tarea para minpularlos. Dos de esas tareas que aparecen continuamente son:

Buscar un elemento: Dado un conjunto de datos \(L=\{x_1,x_2,\ldots,x_n\}\) se trata de comprobar si un cierto objeto \(y\) se encuentra en \(L\) o no.
Ordenar los elementos: Dado un conjunto de datos \(L\) se trata de colocar o mostrar dichos datos como una secuencia \(x_1,x_2,\ldots,x_n\) en la que cada elemento precede al siguiente de modo conveniente (acorde a un orden).

En este tema se muestran algunos algoritmos básicos para resolver los problemas indicados, así como otros algoritmos complementarios que pueden ayudarte a resolver algunos problemas.

2. Algoritmos de búsqueda

2.1. Búsqueda en un array sin elementos ordenados

Para buscar un elemento en un conjunto de datos basta aplicar el siguiente algoritmo:

Seleccionar el siguiente elemento de la lista. La primera vez que se realice este paso, el "siguiente elemento" será el primer elemento de la lista.
Comparar el elemento seleccionado con el elemento a buscar.
Si son iguales, entonces retornar que el elemento ha sido encontrado y parar el proceso de búsqueda.
Si son diferentes y no quedan más elementos en la lista, parar el proceso indicando que la búsqueda no ha tenido éxito.
Pero si son diferentes y aún quedan elementos en la lista, descartar el elemento seleccionado y e ir al paso 1.

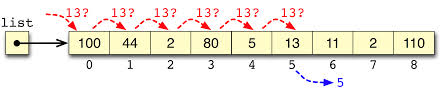
La siguiente figura muestra esta idea. Se busca en el array de enteros list el valor 13. Se encuentra en la sexta posición (índice 5).

Este algoritmo se llama Algoritmo de búsqueda secuencial o de búsqueda lineal (o pura), y en Processing se puede expresar como:

boolean buscar (TipoDato[] lista, TipoDato elemento) {
    int i=0;
    while(i<lista.length)
        if (igual(lista[i], elemento)) return true;
        else i++;
    return false;
}

La clave del algoritmo es qué se entiende por igual(elemento1, elemento2), que dependerá de TipoDato:

Si son tipos de datos simples o String: la función igual() es el operador de comparación ==.
Si son registros: la función igual() consistirá en una función que compara cada uno de los campos del elemento1 con su correspondiente campo del elemento2 y si todos los campos son iguales la función igual() retornará true y en otro caso false. Esta función la tendrás que construir tú.
Si los dos elementos son listas: la función igual() consistirá en una función que compara todos y cada uno de los elementos de ambas listas y para cada índice comparará los elementos respectivos. Si son diferentes, retornará false y si todos los elementos son iguales retornará true. Esta función la tendrás que construir tú.

Observa que el algoritmo se puede modificar fácilmente para que retorne la posición donde se encuentra el elemento encontrado.

En el siguiente código falta la función buscar() para que indique, si existe, la posición de un objeto de tipo Punto en una lista de elementos de tipo Punto. También tendrás que construir la función igual().

class Punto {
    float x;
    float y;
}

void setup() {
    Punto[] ListaPuntos;
    Punto miPunto;
    println(buscar(ListaDePuntos, unPunto);
}

// Construye tus funciones ....

Solución

int buscar (Punto[] aLista, Punto aPunto) {
    if (aLista == null) return -1;
    int i=0;
    while(i < aLista.length)
        if (igual(aLista[i], aPunto)) return i;
        else i++;
    return -1;
}
boolean igual(Punto a, Punto b) {
    if ((a.x == b.x) && (a.y == b.y)) return true;
    return false;
}

2.2. Búsqueda en un array con los elementos ordenados

Cuando los elementos están ordenados la búsqueda se puede optimizar. Si comparo el elemento a buscar, x, con un elemento de la lista, y, como ésta está ordenada, se puede determinar si tengo buscar entre los elementos anteriores a dicho elemento de la lista (si x< y) o si debe de ser de entre los elementos posteriores a dicho elemenos (si (si x> y). Se puede aplicar el siguiente algoritmo:

Establecer variables inf=0 y sup=lista.length-1, como el intervalo de índices de la búsqueda (ambos inclusiven).
Tomar el punto medio del intervalo de búsqueda.
Si el punto medio, con índice centro, coincide con el buscado, retornar que el elemento ha sido encontrado y parar el proceso de búsqueda.
Si el punto medio es mayor que el buscado, "bajar" el límite superior de la búsqueda. Hacer sup=centro-1.
Si el punto medio es menor que el buscado, "subir" el límite superior de la búsqueda. Hacer inf=centro+1.
Si inf> sup, retornar que el elemento no ha sido encontrado y parar el proceso de búsqueda.
Volver al paso 2.

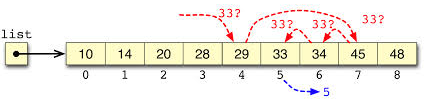
La siguiente figura muestra esta idea. Se busca en el array de enteros list el valor 33. Se encuentra en la sexta posición (índice 5).

Este algoritmo se llama Algoritmo de búsqueda binaria y en Processing se puede expresar como:

boolean buscar (TipoDato[] lista, TipoDato elemento) {
    int inf = 0;
    int sup = lista.lentgh-1;

    while(inf<=sup) {
        centro = (inf+sup)/2;
        if (igual(lista[centro], elemento)) return true;
        if (menor(lista[centro], elemento)) inf = centro + 1;
        else sup = centro - 1 ;
    }
    return false;
}

Al igual que en el algoritmo de búsqueda secuencial se deberá de definir correctamente la función igual(elemento1, elemento2) (ver apartado anterior), y además la función menor(elemento1, elemento2) como sigue:

Si son tipos de datos simples o String, la función menor() es el operador de comparación <.
Si son registros o listas, la función menor() deberás de construir tú de acuerdo a las exigencias de tu problema.

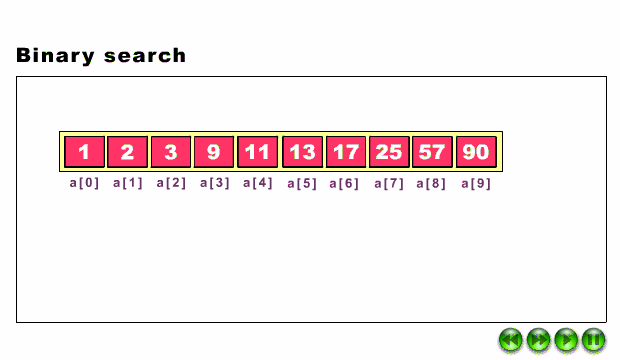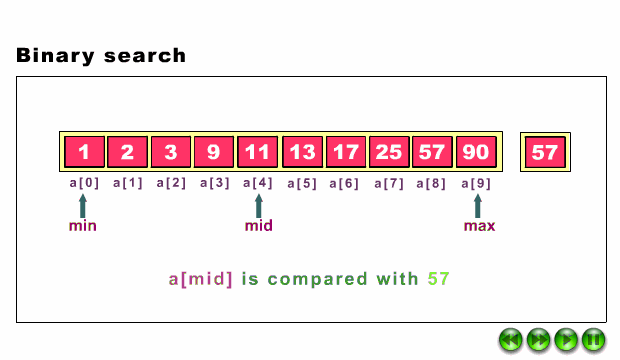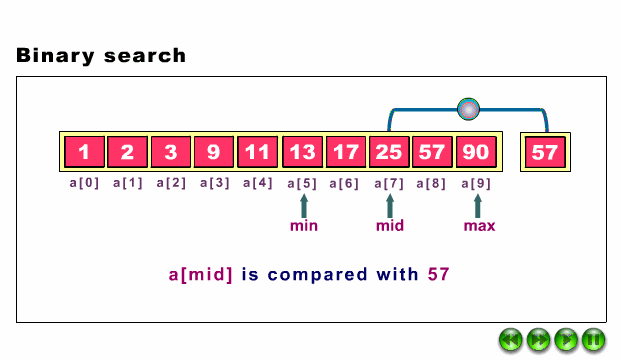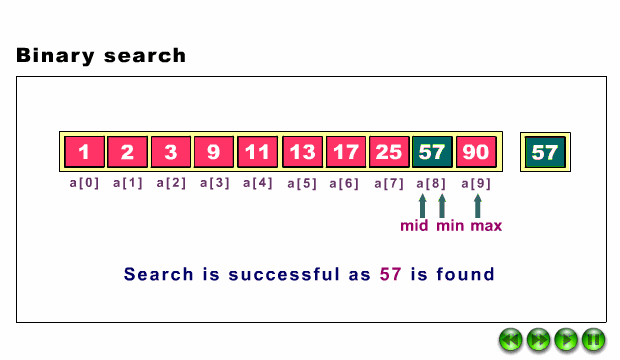
La siguiente animación muestra cómo funciona el algoritmo, por si aún sigues sin verlo claro.

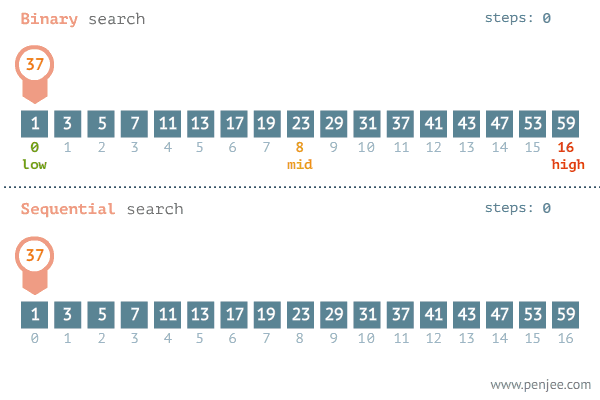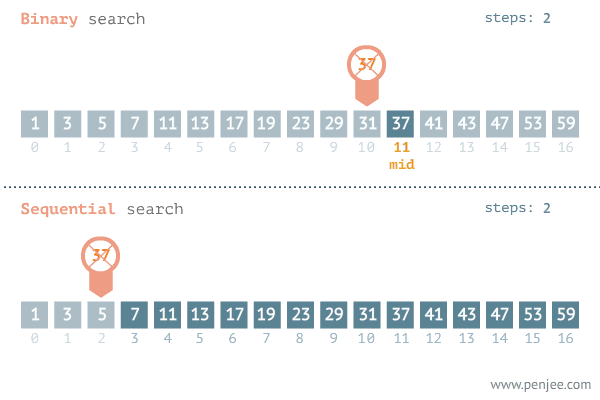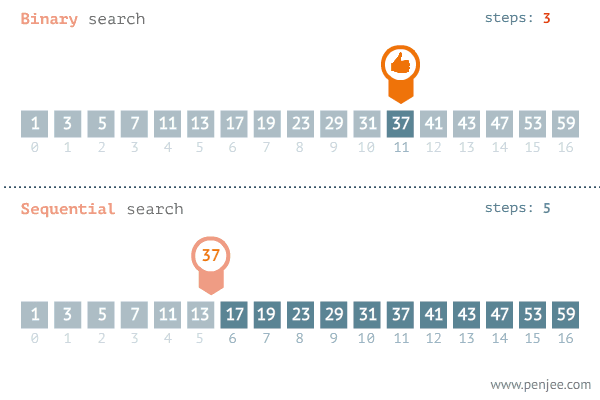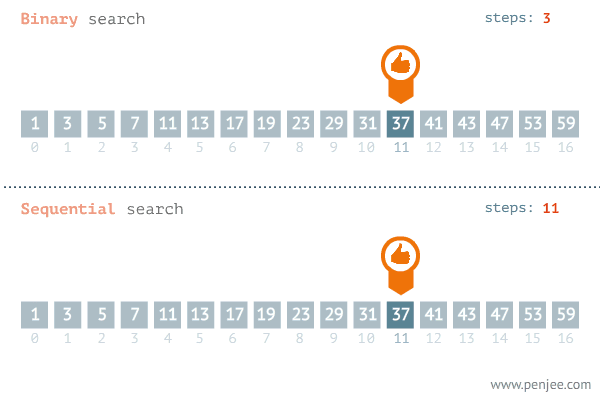
2.3. Búsqueda secuencial vs búsqueda binaria

Observa el comportamiento de los algoritmos buscando el mismo elemento sobre el mismo array.

Lo normal es que el algoritmo de búsqueda binaria encuentre antes el elemento de interés. Pero, a cambio, se necesita invertir un esfuerzo en ordenar la lista de datos, esfuerzo que merece la pena cuando la cantidad de datos es sumamente grande. De ahí que estudiemos la siguiente sección.

3. Algoritmos de Ordenación

Ordenar una lista de datos es un problema muy estudiado en informática. Surge continuamente: la lista ordenada alfabéticamente de los alumnos de una clase, mostrar el ranking de las universidades, mostrar los beneficios empresariales a lo largo del año, etc …

Uno de los alagoritmos más naturales de ordenación es el algoritmo de inserción. Es el que solemos usar cuando ordenamos las cartas de una baraja por orden numérico.

La idea es simple. Se considera un elemento de la lista y se mira todos los elementos que están a su izquierda. Entonces dicho elemento se colocará justo a continuación del primer elemento que sea más pequeño a él. Para ello es necesario que cuando se seleccione un elemento de la lista todos los que están a su izquierda ya deben de estar ordenados entre sí.

Ejemplo 1. Un ejemplo animado del algoritmo de inserción

Una demostración del algoritmo de inserción que ordena en orden creciente la secuencia de números {6,5,3,1,8,7,2}.

Para aplicar el algoritmo de ordenación por inserción se requiere de lo siguiente:

Datos de entrada

vec, el vector de datos que se desea ordenar.
tam, tamaño del vector. Los subíndices válidos van desde 0 hasta tam-1 inclusive.

Variables intermedias

pos, posición del elemento a comparar.
posAnterior, variable que recorre todos las posiciones anteriores a pos (hasta la primera)

Funciones

intercambiar(a, b), intercambia los valores de las variables a y b.

Con ello, en lenguaje algorítmico se puede expresar como sigue:

  ordenaciónInserción(vec)
    tam = length(vec)

    Desde pos=1 hasta tam-1 inclusive hacer

      valor = vec[pos]
      posAnterior = pos - 1

      Mientras posAnterior >= 0  AND vec[posAnterior] > valor hacer
          intercambiar(vec[posAnterior+1], vec[posAnterior])
          posAnterior = posAnterior - 1
      Fin (Mientras)

      vec[posAnterior + 1] = valor

    Fin (For-pos)

Implementa el algoritmo de ordenación por inserción para un array de enteros.

Otro algorimo de ordenación es el basado en el método de la burbuja, consistente en ir recorriendo todas y cada una de las posiciones y comparar el valor que almacena con la posición inmediatamente siguiente para colocar el mayor valor de la pareja en la mayor posición. La primera vez que se realiza este proceso el mayor valor estará en la última posición del array, la segunda vez el penúltimo mayor estará en la última posición del array, y así sucesivamente. En lenguaje algorítmico se puede expresar como sigue:

  ordenaciónBurbuja(vec)
    tam = length(vec)

    Desde i=1 hasta tam-1 inclusive hacer
      Desde pos=0 hasta tam-1-i inclusive hacer

        si vec[pos] > vec[pos+1] entonces
           intercambiar(vec[pos], vec[pos+1])

      Fin (For-pos)
    Fin (For-i)

Ejemplo 2. Un ejemplo animado del algoritmo de burbuja

Una demostración del algoritmo de burbuja que ordena en orden creciente la secuencia de números {6,5,3,1,8,7,2}.

Existen otros algoritmos básicos como el de ordenación por selección. Búscalo y completa este documento.

4. Repaso

Un array es una estructura formada por una lista de valores, todos del mismo tipo.
Antes de usar una variable de tipo array siempre hay que usar la instrucción new TipoDato[n], siendo n el número de elementos que contendrá la lista.
Si TipoDato es una estructura de datos, será necesiario realizar la correspondiente reserva de memoria para cada elemento de la lista.
- Si TipoDato es un registro, será: lista[i] = new TipoRegisto()
- Si TipoDato es un array, será: lista = new Tipo[n][m]
El acceso de cada elemento de lista[i] será acorde al tipo de dato:
- Si TipoDato es un registro, lista[i].campo permite acceder al campo campo del registro i-ésimo.
- Si TipoDato es un array, lista[i][k] permite acceder al elemento k-ésimo de la lista lista[i].