Límites de funciones de una variable, y diferenciales de una o varias variables

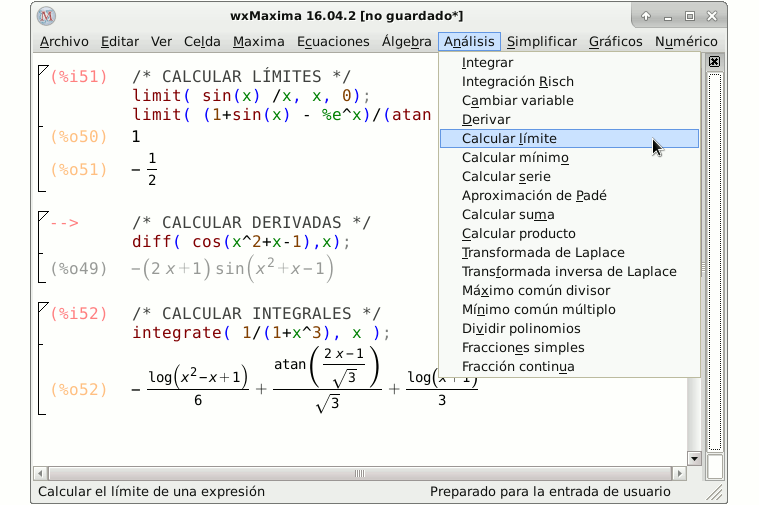
Límites para funciones de una variable
Derivadas y diferenciales

Límites, derivadas, integrales con wxmaxima

Límites para funciones de una variable

Maxima tiene la posibilidad de calcular límites de funciones de una variable en un punto utilizando:

limit(Función, Variable, Punto, Dirección);
tlimit(Función, Variable, Punto, Dirección);
es análogo al anterior pero usa desarrollos de Taylor para evaluar los límites.

El argumento Dirección es opcional y sus valores son plus para el límite por la derecha y minus para el límite por la izquierda.
El comando utiliza los siguientes símbolos especiales inf para infinito positivo y ninf para infinito negativo.
En la salida, eventualente pueden obtenerse los siguientes resultados: und (indefinido), ind (indefinido pero acotado) y infinity (infinito complejo).
La técnica utilizada es la que corresponde a la regla de L'Hospital y para evitar situaciones indeseables es posible fijar mediante la variable lhospitallim el número máximo de reiteraciones de la regla de L'Hospital (el valor por defecto es 4).

limit( 1/(1+x^2), x, inf);
limit( (1+sin(x) - %e^x)/(atan (x)*atan (x)), x, 0);
limit( %e^(1/cos(x)), x, %pi/2,plus);
limit( %e^(1/cos(x)), x, %pi/2,minus);
tlimit( 1/(1+x^2), x, inf);
tlimit( (1+sin(x) - %e^x)/(atan (x)*atan (x)), x, 0);
tlimit( %e^(1/cos(x)), x, %pi/2,plus);

Derivadas y diferenciales de una o varias variables

Para el cálculo diferencial de una y varias variables Maxima dispone de del comando diff cuya sintaxis depende del número de variables:

diff(Función de una variable, Variable, Veces)
Calcula la derivada de una Función que depende de la Variable el número de Veces indicado. El número Veces puede eludirse si es uno. Si aparecen otras variables en Función son consideradas como constantes.
diff(Función de varias variables Variable1, Veces1, Variable2, Veces2,...)
Calcula la derivada parcial del orden indicado para cada una de las variables que se seleccionan. Si aparecen otras variables, son consideradas como constantes.
diff(Función)
Calcula la diferencial cuando se declara en la Función las variables de las que depende; si sólo depende de una variable calcula la derivada.

Algunos ejemplos que ilustran lo anteriormente descrito:

Los primeros ejemplos son de funciones concretas con variables identificadas
diff( sin(x), x);
diff( cos(x),x,2);
diff( y*cos(x),x,2);
diff( y*cos(x),x,2,y,1);
kill(f)$ diff( f(x,y),x,1,y,2); diff( exp(f(x)), x,2);
diff( f(x,y) );
del(Variable) representa la diferencial de esa variable, digamos dx, dy,...
Es posible hacer la diferencial de un "símbolo" genérico (que corresponde a una función) cuyas variables se declaran con el comando
depends(símbolo,lista variables)
depends(F,[x,y])$ diff( F );
/* diferencial de funciones escalares */ diff( y*cos(x) ); diff( y*cos(x)+z^2 );
/* diferencial de una función vectorial */ g(x,y):=[x^3,x^2+y^2,exp(x+y)]; diff(g(x,y));
Siguen algunas derivadas simbólicas (anteponer apóstrofo) y su evaluación (anteponer apóstrofo doble):
'diff(x^2*cos(x^3),x)= ''diff(x^2*cos(x^3),x); 'diff(x^2*cos(x^3),x,3)=''diff(x^2*cos(x^3),x,3); 'diff(exp(x^2+y),x,2,y,1)= diff(exp(x^2+y),x,2,y,1);

jacobian(Lista Funciones, Lista Variables)
Devuelve la matriz jacobiana (derivadas parciales de orden 1) de la Lista Funciones respecto de la Lista Variables.
Es necesario utilizar [ ] aunque solamente haya una Función en la lista.
Cuando en la Lista Funciones solamente hay una, la matriz corresponde al vector gradiente.
hessian(Función, Lista Variables)
Devuelve la matriz hessiana de la Función respecto de la Lista Variables, es decir, la matriz de las derivadas parciales de orden 2 respecto de todas las variables.

f(x,y):= -(x^2+y^2); jacobian([f(x,y)],[x,y]); ev(%,x=1/2,y=1/2);
kill(f)$ jacobian([f(x,y)],[x,y]);
jacobian ([sin (u - v), sin (u * v)], [u, v]);
jacobian ([F(x,y), G(x,y)],[x,y]);
hessian (x * sin (y), [x, y]);
depends (F, [x,y]); hessian (F, [x, y]);

En los ejemplos anteriores se han utilizado funciones elementales cuyo nombre en Maxima coincide con el usual. Puede consultar una lista de funciones que Maxima conoce y también la forma de definir nuevas funciones.