Indice Derecha

 

Introducción

Maxima es un sistema para la manipulación de expresiones simbólicas y numéricas, incluyendo diferenciación, integración, desarrollos en series de Taylor, transformadas de Laplace, ecuaciones diferenciales ordinarias, sistemas de ecuaciones lineales, vectores, matrices. Maxima produce resultados con alta precisión usando fracciones exactas y representaciones con aritmética de coma flotante arbitraria y puede también realizar gráficas de funciones, y de datos, en dos y tres dimensiones. Los procedimientos pueden ser programados y entonces ejecutar Maxima para realizar tareas complejas.

El sitio oficial de Maxima es http://maxima.sourceforge.net. Podrá encontrar allí el código fuente y el manual de Maxima junto con otras informaciones. Como curiosidad: gran parte de la sintaxis de otros programa, como Maple y Mathematica, fue copiada de Maxima.

 

Instalación

En la página oficial http://maxima.sourceforge.net/download.html pueden encontrarse los programas y la información necesaria para instalarlos dependiendo del sistema operativo.

En el caso de los sistemas GNU-Linux lo más confortable es utilizar los repositorios oficiales y hacer la instalación en la forma estándar para esa distribución. A modo de ejemplo, como usuario de Debian que soy, yo me limito a abrir una consola adquirir los privilegios de root y ejecutar en ella el siguiente código
apt-get install xmaxima wxmaxima

 

Modus operandi

En lo sucesivo emplearemos el término "sentencia" o "comando" para referirnos a las órdenes o instrucciones que Maxima reconoce y las que se obtienen ciertos resultados. El programa xMaxima tiene dos ventanas de trabajo. Una console o "ventana de ejecución de Maxima", en donde se van introduciendo las sentencias y obteniendo los resultados. Y otra "ventana de navegación", que es un navegador especial para documentos html que tienen capacidad de ejecutar cóodigo de Maxima que se utiliza para navegar por el manual original de Maxima o para ir leyendo un guión de prácticas con Maxima del tipo de este "Manualico".

Si está leyendo este documento con un navegador estándar podrá distinguir los ejemplos de sentencias Maxima que incorpora al estár escritas sobre fondo azul. Marcando y copiando dichas sentencias desde su navegador preferido, podrá insertarlas luego en cualquier interfaz capaz de ejecutar código Maxima.

Pero este documento ha sido diseñado también para ser leído en la "ventana de navegación" de xMaxima, y en tal caso el fondo desaparecerá pero las sentencias Maxima de tales ejemplos aparecerán resaltadas en azul indicando de ese modo que se convierten en enlaces interactivos para Maxima: un doble click de ratón sobre ellas tendrá el efecto de ejecutarlas, como si hubiesen sido escritas manualmente en la "ventana de ejecución de Maxima". Además podrá modificar interactivamente el texto desde la "ventana de navegación" (a diferencia de lo que ocurre con un navegador estándar) y volver a ejecutar el código modificado.

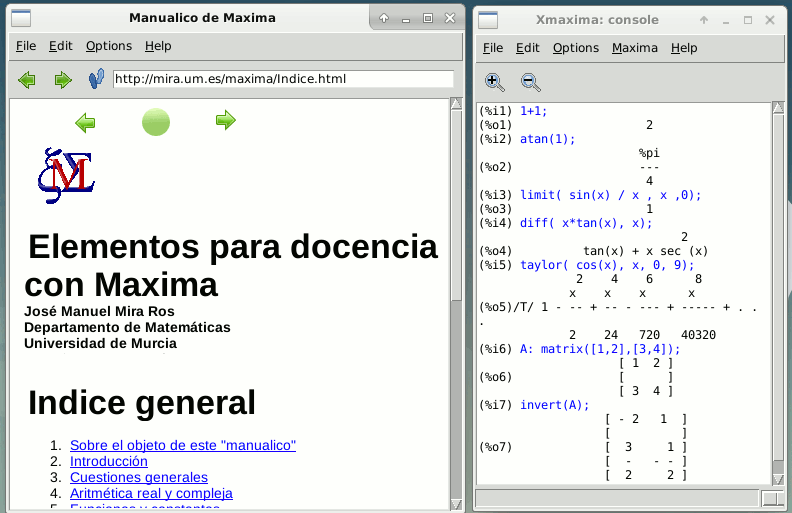
xMaxima

La imagen situada encima muestra una sesión de xMaxima con las ventanas de navegador y consola. En la ventana del navegador es necesario escribir "a mano" la dirección url a la que queremos conectar, que puede ser un documento local o un documento de la red.

Entre los varios interfaces para interactuar con Maxima que existen, la imagen que aparece a continuación corresponde a una captura de pantalla de la interfaz xwMaxima que resulta muy ergonómica para trabajar con Maxima.

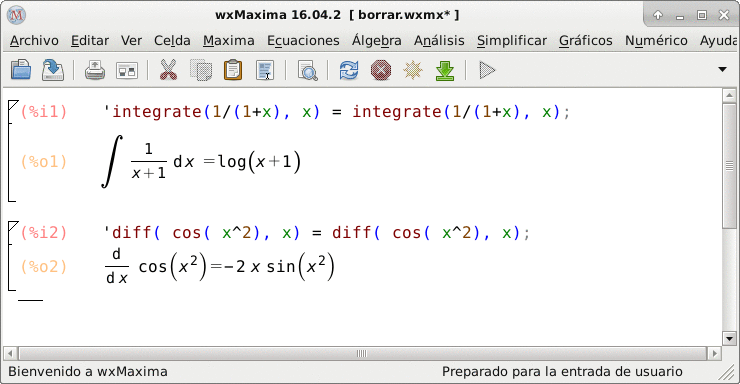
wxMaxima

 

(%i1) es una etiqueta que identifica una sentencia de Maxima mediante un contador que se va incrementando de forma automática y una letra que indica si se trata de una sentencia de entrada (input) (%i1) (%i2),... o de salida (output) identificada con (%o1), (%o2).

Para realizar operaciones básicas se escribe la correspondiente línea de código finalizando con punto y coma ;
y a continuación se ejecuta "Retorno de Carro" ("Mayúscula+Retorno de Carro" en el caso de wxMaxima).

El punto y coma se utiliza también para separar instrucciones escritas en un mismo renglón. Puede probarlo copiando una a una las sentencias que aparecen más abajo y pegándolas en la ventana de ejecución de Maxima, ya sea ésta la ventana superior de xMaxima o un servidor de internet en el que pueda ejecutarse dichas sentencias.

  1. 1+1;
  2. 3*5;
  3. 9/3;
  4. x:9; y:3; x*y;

A veces puede suceder que sea necesario utilizar un comando para realizar un cálculo intermedio, que o bien es irrelevante o se quiere explícitamente evitar que aparezca en la pantalla. En tales casos puede acabarse la sentencia con el simbólo de dólar $ en lugar de con ;

x:9$ y:3$ z:2$ x*y*z; kill(all)$

El último comando kill(all) anula las asignaciones realizadas anteriormente para las variables x, y, z (y todas las demás asignaciones que se hubieran realizado). Es algo a tener en cuenta porque si luego queremos calcular la derivada del cos(x) tenemos problemas porque x se ha convertido en una constante.

Si está leyendo este documento desde xMaxima, haciendo doble click encima de cada una de las sentencias podrá comprobar que la sentecia se ejecuta y el resultado obtenido aparece en la console (ventana para escribir y ejecutar código Maxima), con la numeración correlativa que corresponda. También podrá verificar que puede modificar interactivamente el texto en azul y, con un doble click, ejecutar la nueva sentencia. Por supuesto, esto no es posible hacerlo con un navegador estandar.

Vamos a acabar esta introducción con algunos ejemplos de cálculo numérico, simbólico y grafismo que sirvan hacerse una idea de la sintaxis y de la forma en que opera Maxima. En cada caso explicamos con un comentario sucinto el objetivo del ejemplo; Maxima ignora tales comentarios.

  1. /* derivada del coseno */ diff(cos(x),x);
  2. /* desarrollo de Taylor del coseno en 0 hasta el grado 5 */ taylor(cos(x),x,0,5);
  3. /* primitiva de 1/(1+x^2) con variable x */ integrate(1/(1+x^2),x);
  4. /* integral de 0 a 1 de la función precedente */ integrate(1/(1+x^2),x,0,1);
  5. /* definir una matriz M mediante sus filas */ M:matrix([1,x],[2,y]);
  6. /* cálculo del determinante de M */ determinant(M);
  7. /* y ahora la matriz inversa de M */ M^^(-1);
  8. /* resolver un sistema lineal con dos variables */ solve([2*x-y=3,x-7*y=0],[x,y]);
  9. /* dibujar una función de una variable en un intervalo */ plot2d(x^3-3*x+1, [x,0,2]);
  10. /* dibujar una función de dos variables */ plot3d(x^2 - y^2, [x,-1,1], [y,-1,1]);
  11. /* encontrar las raíces reales (aproximadas) de un polinomio */ realroots(x^3-3*x+1);
  12. /* resolver una ecuación */ solve(x^4=1,x);

 

Como ya se ha mencionado, este Manualico puede ser abierto con un navegador estándar o con el navegador de xMaxima, pero el comportamiento no es el mismo con ambos. En lo sucesivo el icono que inicia esta línea ubicado en algún lugar del texto significa que el hiperenlace que va a continuación no puede ser ejecutado desde el navegador de xMaxima.

Indice Derecha