Para Maxima un vector es sólo una lista: la lista de sus coordenadas. En consecuencia, es de aplicación todo lo indicado en el apartado Listas que tenga sentido en este tipo de lista.
Maxima no implementa de forma nativa un comando para calcular la norma de un vector, pero es sencillo crearlo utilizando el producto escalar:
Mediante comandos de Maxima se pueden construir matrices de varias formas. Y también los interfaces para trabajar con Maxima (por ejemplo wxMaxima) pueden aportar herramientas visuales que facilitan la construcción de las mismas.
Pueden realizarse diferentes operaciones con matrices, las más básicas están simbolizadas del siguiente modo:
Otras operaciones frecuentes con matrices (calcular la transpuesta, la inversa, el determinante,...) están contempladas en los comandos de Maxima.
- transpose(Matriz)
Calcula la transpuesta
A : matrix([1,2,3],[4,8,5],[9,5,4]);
print("su transpuesta es ", transpose(A));
- adjoint(Matriz)
Calcula la adjunta
A : matrix([1,2,3],[4,8,5],[9,5,4]);
print("su adjunta es ", adjoint(A));
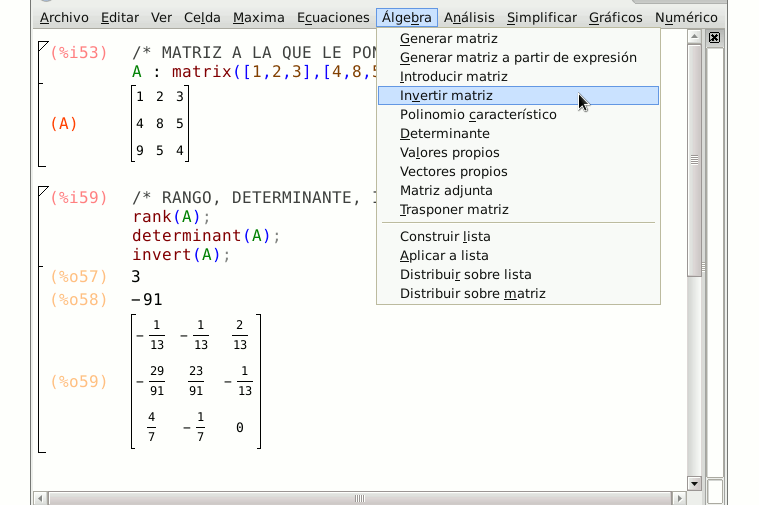
- invert(Matriz)
Calcula la inversa utilizando el método de los adjuntos
A : matrix([1,2,3],[4,8,5],[9,5,4]);
print("su inversa es ", invert(A));
- invert(Matriz),detout
Calcula la inversa con el determinante fuera
A : matrix([1,2,3],[4,8,5],[9,5,4]);
invert(A),detout;
- determinant(Matriz)
Calcula el determinante de una Matriz
A : matrix([a,b,c],[d,e,f],[g,h,i]);
determinant(A);
expand(%);
- rank(Matriz)
Calcula el rango
A : matrix([1,2,3],[4,8,5],[3,6,2]);
print("Determinante de A = ", determinant(A))$
print("Rango de A = ",rank(A))$
- minor(Matriz,i,j)
Calcula el menor (i,j) de Matriz, esto es, elimina la fila i y la columna j de Matriz
A : matrix([9,2,4],[4,8,5],[1,2,0]);
minor(A,2,2);
- triangularize(Matriz)
Genera una matriz triangular superior como la que produce el algoritmo de Gauss.
echelon(Matriz)
Es una "normalización" del comando anterior obtenido al multiplicar cada fila por el inverso del primer coeficiente no nulo.
A : matrix([9,2,4],[4,8,5],[0,1,8]));
triangularize(A);
echelon(A));
- charpoly(Matriz, Variable)
Escribe el polinomio característico respecto de la Variable fijada
A : matrix([9,2,4],[4,8,5],[0,1,8]);
charpoly(A,x);
expand(%);
- mattrace(Matriz)
Calcula la traza de la matriz cuadrada Matriz (suma de los elementos de la diagonal principal)
- eigenvalues(Matriz)
Calcula los valores propios de la Matriz indicando la multiplicidad de los mismos. Lo hace a través de una lista doble: en la primera están los valores propios, en la segunda sus multiplicidades. eivals es un sinónimo.
Este comando llama a la función solve para encontrar las raíces del polinomio característico, aunque en ocasiones no es capaz de encontrarlas. En tales casos, la utilización de algsys permite obtener soluciones aproximadas mediante
algsys([charpoly(A,x)=0],[x]);
A : matrix([9,2,4],[4,8,5],[0,1,8]);
eigenvalues(A);
- eigenvectors(Matriz)
Devuelve una lista con 2 sublistas. La primera la
forman los valores propios con sus multiplicidades, la segunda está
formada por los correspondientes vectores propios
- uniteigenvectors(Matriz) ueivects(Matriz)
Ambos calculan los vectores propios unitarios de la Matriz
A : matrix([9,2,4],[4,8,5],[0,1,8]);
ueivects(A);
- nullspace(Matriz)
Calcula una base para el espacio vectorial correspondiente al núcleo de la aplicación lineal que define la Matriz. Un resultado span() significa que el núcleo es 0 (aplicación inyectiva).
A : matrix([9,2,4],[4,8,5],[0,1,8]);
nullspace(A);
- columnspace(Matriz)
Calcula una base para el espacio vectorial de las columnas de la Matriz.
A : matrix([1,2,3],[4,5,6],[7,8,9]);
columnspace(A);

Sistemas de ecuaciones lineales
Es conocida la relación existente entre las matrices y los sistemas de ecuaciones lineales, para cuya resolución Maxima implementa el comando
- linsolve ([EC_1, ..., EC_m], [x_1, ..., x_n]);
Permite resolver sistemas de ecuaciones lineales en varias variables.
Las ecuaciones EC_1...EC_m son polinomios de primer grado en las variables x_1,...x_n con dos miembros separados entre sí por el signo =. Pero también es posible escribir el polinomio sin incluir un sigo =, en cuyo caso se añadirá internamente =0 para convertir el polinomio en una ecuación.
- coefmatrix([EC_1, ..., EC_m], [x_1, ..., x_n]);
Recupera la matriz de los coeficientes a partir de un sistema de ecuaciones y de ese modo facilita el tratamiento matricial del sistema.
- augcoefmatrix([EC_1, ..., EC_m], [x_1, ..., x_n]);
Devuelve la matriz aumentada de coeficientes del sistema de ecuaciones lineales de variables x_1, ..., x_n con los términos independientes de cada ecuación.
- list_matrix_entries(Matriz);
Tiene la finalidad contraria: convertir la matriz en listas a las que poder aplicar comandos de tipo solve y linsolve
Primera ilustración: sistema compatible y determinado. La solución existe y es única.
- linsolve([2*x+y+3*z=1, -4*x+2*y-z=2, 5*x+y+2*z=3], [x,y,z]);
- linsolve([2*x+y+3*z-1, -4*x+2*y-z-2, 5*x+y+2*z-3],[x,y,z]);
El mismo sistema escrito en la forma =0, que Maxima da por sobrentendido si no aparece el signo =
- eqs:[x+y+2*z=4,-2*x-2*z+2*t=-2,3*x+2*y+5*z-t=9,4*x+y+5*z-3*t=7]$
linsolve(eqs,[x,y,z,t]);
Un sistema que no tiene solución única
El problema podría haber sido abordado también como la resolución de una ecuación matricial del tipo A . X = B donde A y B son conocidos y X es la incognita. En el caso de que la matriz sea invertible basta multiplicar la ecuación anterior por la inversa de A para obtener X
print("Definimos las matrices")$
A : matrix([2,1,3], [-4,2,-1], [5,1,2]);
X : transpose( matrix([x,y,z]) );
B : transpose( matrix([1,2,3]) );
print("Se trata de resolver", 'A . 'X = 'B)$
print("para lo cual empezamos analizando si la matriz tiene inversa")$
is( determinant(A) # 0 );
(invert(A) . A) . X = invert(A) . B;
Visto que la matriz era invertible al ser su determinante no nulo, hemos multiplicado a izquierda la ecuación
A.X=B por invert(A) a fin de despejar X.
Una vez comprobado que el determinante no se anula, resulta tentador, para quien lo conoce
(Resolver Ecuaciones) utilizar el comando solve;
pero de ese modo no funciona; el motivo es que para Maxima matrices y listas son conceptualmente diferentes,
aunque estén relacionadas.
- A . X = B;
- A . X - B;
- solve( A . X - B , X );
Escrito así no salve resolverlo. Pero transformando las matrices en listas sí sabe hacerlo:
- solve( list_matrix_entries(A . X - B) , list_matrix_entries(X) );
Segunda ilustración: sistema compatible e indeterminado. Existen infinitas soluciones diferentes.
Modificamos ligeramente la matriz precedente
- M: matrix([2,1,3],[-4,2,-1],[-2,3,2]);
determinant(M);
Como ahora el determinante es nulo, no podemos usar la técnica anterior.
Pero sí podemos calcular el rango de la matriz y un menor de rango máximo:
- rank(M);
M1 : submatrix(3,M,3);
rank(M1);
B;
Por tanto la tercera fila de M es una combinación lineal de las anteriores. De hecho, es la suma de los dos primeras, y lo mismo ocurre con la matriz B (de no ser así el sistema sería incompatible), lo cual hace posible que nos centremos únicamente en las dos primeras filas y aplicar la tecnología del ejemplo anterior a la matriz M1, considerando que las únicas incognitas son x y pasando la z a ser un parámetro libre.
Podríamos continuar por ese camino; o, alternativamente aplicar triangularize a la matriz orlada, que no es muy diferente...
Pero no lo vamos a hacer, porque Maxima es capaz de realizar por sí mismo ese análisis y de resolver el sistema (compatible pero indeterminado) con la tecnología solve anteriormente usada:
solve( list_matrix_entries(M . X - B), list_matrix_entries(X));
Obsérvese que la solución depende de un parámetro libre.
Interfaz de wxmaxima

 Ap_Matrices.wxmx
Ap_Matrices.wxmx
 Ap_SistemaLineal.wxmx
Sistema de ecuaciones con un parámetro
Ap_SistemaLineal.wxmx
Sistema de ecuaciones con un parámetro















