Schrödinger: Escalón de potencial

La ecuación de Schrödinger en una dimensión viene dada por:
 

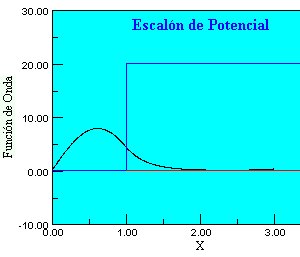
Estudiemos el caso de una partícula que se encuentra sometido a un potencial que es infinito en el origen y tiene forma de escalón para una distancia unidad. El potencial U(x) sera cero en el interior del pozo, 0 < x < L y fuera de él es infinito para valores de x < 0 y un valor finito para valores de x > L por lo que la función de ondas debe valer cero en x = 0 y en L la función y su derivada debe ser continuas. Con las consideraciones anteriores, para puntos entre 0 y L con U = 0, podemos escribir: f [i+1] = (2.0 - delta² ∗ E) ∗ f [i] - f [i-1]; y para puntos con x > L f [i+1] = (2.0 - delta² ∗ (E-U)) ∗ f [i] - f [i-1]; donde: delta = L/N N número de puntos en el que dividimos L.

Dando un valor para la energía E y el valor inicial para la función f [0] = 0 y un valor arbitrario, razonablemente pequeño, para el siguiente valor de la función por ejemplo f [1] = 0.1, imponemos la condición de que la función y su derivada sean continuas en L:

La condición para que la derivada sea continua en N vendrá dada por:

de donde obtenemos la condición de frontera:

y variamos la energía E hasta comprobar que la función tiende asintóticamente a cero para valores mayores de L, cuando esto sea así ese valor de E es uno de los valores buscados para la energía.

En el siguiente enlace se puede ver un ejemplo de una Simulación realizada con EJSen la que podemos modificar facilmente la energía y comprobar para que valor esta se vuelve a hacer cero.

Cálculo Numérico >>  Discretización de ecuaciones diferenciales >>  Ecuación de Schrödinger >>  Escalón de potencial