Perturbación armónica

La forma de las ondas es muy variada, hay un caso de especial interés, si el emisor de la onda varía armónicamente con el tiempo la onda que se genera es una función armónica del tiempo y del espacio.

http://webs.um.es/jmz/IntroFisiCompu/ejs/Ejemplos/drawables/onda_periodica.html

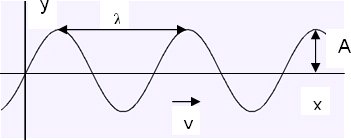
En la imagen podemos observar una fotografía de este tipo de ondas. Vamos a llamar longitud de onda λ a la distancia entre los puntos más próximos con igual valor de la perturbación y período T al tiempo que un punto tarda en recuperar un valor dado de la perturbación.

Supongamos que proponemos esta ecuación como representación de esta onda:

Veamos qué significa k, tomemos dos puntos que, en un cierto instante t se encuentren separados una longitud de onda λ, por la definición que hemos dado ambos puntos tendrán igual valor de la perturbación.

Imponiendo esa condición llegamos a

De modo similar dejemos que para un punto x pase un período T.

A k se le llama número de onda y está relacionado con la longitud de onda. Podemos escribir nuestra ecuación para las ondas armónicas como:

En donde aparece explícitamente la dependencia con la longitud de onda λ y el período T.

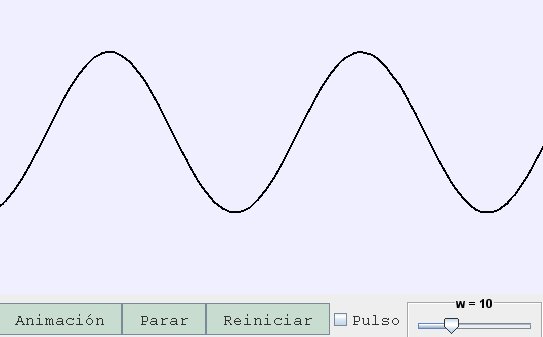
En la siguiente simulación se puede estudiar la relación entre estas magnitudes y la velocidad de propagación de la perturbación.

Energía transportada por una onda que viaja por una cuerda.

La energía media transportada por una señal periódica en una cuerda en un segmento viene dada por la expresión:

Esta expresión se obtiene teniendo en cuenta las energías cinéticas y potenciales de este segmento, aunque para cada tipo de onda la expresión de la energía lógicamente variará, es relevante señalar la dependencia de la energía con la amplitud y la frecuencia de la señal.