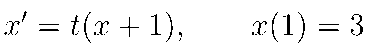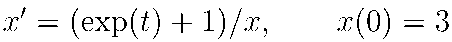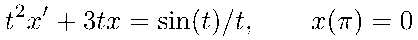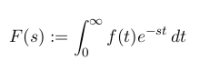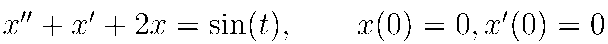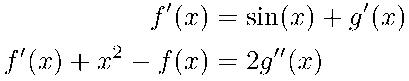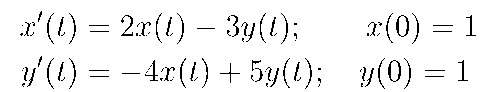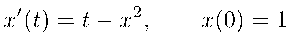Ecuaciones diferenciales

Soluciones analíticas con ode2
Maxima puede obtener soluciones analíticas de ciertos tipos de ecuaciones diferenciales
ordinarias (ODE) de primer y de segundo orden. Sin embargo, actualmente, Maxima en este tema no alcanza las prestaciones de algunos CAS comerciales.
Puede resolver:
- Primer orden de los tipos:
lineales, de variables separables, homogéneas, de Bernoulli, exactas (incluso mediante la
introducción de un factor integrante).
- Segundo orden de los tipos: exactas, lineales con coeficientes constantes o reducibles a ellas,
de Euler y aquellas que no contienen una de las variables. Por comodidad en la formulación de los comandos, denotaremos la variable con t y la función con x
- ode2(ecuación diferencial,x,t).
Es el comando a usar para todos los tipos antes indicados.
Atención en la ecuación diferencial se escribe x no x(t) a diferencia de lo que luego veremos con otros comandos.
Cuando tiene éxito, Maxima devuelve la solución general explícita o implicita utilizando %c para representar la constante de integración en las de primer orden y %k1 %k2 para las de segundo orden.
Cuando no puede obtener la solución devuelve false, posiblemente con algún mensaje de error.
- ic1(solución general,t= valor inicial, x= valor inicial)
Para las ecuaciones diferenciales de orden uno, aplica a la solución general las condiciones iniciales y obtiene la solución particular.
- ic2(solución general,t= valor inicial,x= valor inicial, 'diff(x,t)= valor inicial)
Para las ecuaciones diferenciales de orden dos, aplica a la solución general las condiciones iniciales y obtiene la solución particular.
- bc2(solución general,t= t_1,x= x_1, t= t_2,x= x_2)
Para las ecuaciones diferenciales de orden dos, aplica a la solución general las condiciones frontera (debe pasar por los puntos (t_1,x_1) y (t_2,x_2)) y obtiene la solución particular.
Veamos algunos ejemplos. Llamamos la atención sobre el uso del apóstrofo para escribir la ecuación y la identificación de las variables dependiente e independiente.
Empezamos con las de primer orden:
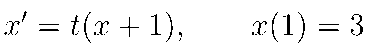
/* ponemos nombre a la ecuación */
E1 : 'diff(x,t)=t*(x+1);- /* calculamos la SOLUCIÓN GENERAL y le ponemos nombre */
SGE1: ode2(E1,x,t),fullratsimp;
- /* CONDICIÓN INICIAL: solución particular que cumpla x(1)=3 */
ic1(SGE1,t=1,x=3);
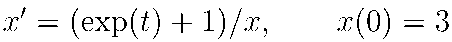
kill(all)$
E1:'diff(y,t)=(exp(t)+1)/y;
ode2(E1,y,t);
ic1(%,t=1,y=3);
solve(%,y); 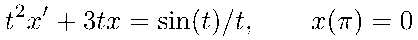
kill(all)$
E1 : t^2*'diff(x,t)+3*t*x=sin(t)/t;
SGE1 : ode2(E1,x,t);
ic1(SGE1,t=%pi,x=0);
Y ahora las ecuaciones de segundo orden. Obsérvese la forma en que se indican las condiciones iniciales: en este caso la variable independiente es t y la variable dependiente es x.

kill(all)$
E1 : 'diff(x,t,2)-'diff(x,t)*10 +9*x=5*t;
SGE1 : ode2(E1,x,t);
ic2(SGE1,t=0,x=-1,'diff(x,t)=2);
kill(all)$
E1 : 'diff(x,t,2) -10* 'diff(x,t) + 9*x = 5*t;
SGE1 : ode2(E1,x,t),fullratsimp;
bc2( SGE1,t=0,x=-1, t=1,x=2);

Soluciones con contrib_ode
El comando contrib_ode, implementado en el paquete del mismo nombre que ha de ser cargado previamente, extiende las posibilidades de ode2 con métodos adicionales para ecuaciones diferenciales ordinarias lineales y no lineales de primer orden y homogéneas lineales de segundo orden.
El código se encuentra en estado de desarrollo y la sintaxis puede cambiar en futuras versiones.
- contrib_ode(ecuación diferencial,x,t).
La sintaxis de uso es la misma que la de ode2. Si consigue encontrar la solución devuelve una lista de soluciones, ya que las ecuaciones no lineales pueden tener múltiples soluciones.
La solución puede venir dada de forma explícita, implícita o paramétrica en términos de la variable %t; incluso el resultado puede ser una transformación de la ODE original en una nueva ODE con variable %u
%c es la notación para la constante de integración para ODEs de primer orden y %k1, %k2 para las de segundo orden.
- method
Indica el método aplicado en la resolución
- contrib_chek(ecuación , solución)
Devuelve el valor de la ecuación tras sustituir en ella una posible solución. El valor es cero si realmente es una solución de la ecuación.
- /* soluciones en la consola */ kill(all)$ load(contrib_ode)$
- E1 : t^2*'diff(x,t)+3*t*x=sin(t)/t;
SGE1 : contrib_ode(E1,x,t);
ic1(SGE1,t=%pi,x=0);
- E2 : t*(t+1)*'diff(x,t,2)+(t+5)*'diff(x,t,1)+(-4)*x;
print("Resolución con ode2:", ode2(E2,x,t))$
contrib_ode(E2,x,t);
bc2( %[1], t=1,x=2, t=2,x=3);
Los resultados muestran que el comando contrib_ode resuelve ecuaciones que ode2 no es capaz de resolver.
- E3 : 'diff(y,x,2)+(a*x+b)*y;
S3 : [y = bessel_y(1/3,2*(a*x+b)^(3/2)/(3*a))*%k2*sqrt(a*x+b)
+bessel_j(1/3,2*(a*x+b)^(3/2)/(3*a))*%k1*sqrt(a*x+b)];
print("Veamos si S1 es solución de la ecuación E1, lo cual corresponde
a que la respuesta sea 0. En este caso la respuesta es: ",
ode_check(E3,S3[1]))$

Soluciones analíticas usando la transformada de Laplace
La transformada de Laplace de una función f(t), en caso de existir, es la función F(s) definida mediante la fórmula
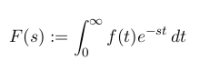
Una propiedad muy importante en las aplicaciones es que, en condiciones bastante generales, se trata de operador que es inyectivo (teorema de Lerch), lo cual significa que si dos funciones tienen la misma transformada de Laplace entonces las funciones coinciden. Esto permite hablar de la transformada de Laplace inversa, la cual resulta muy útil para la resolución de algunas ecuaciones diferenciales.
- laplace(f(t),t,s)
Es el comando a utilizar para realizar la Transformadas de Laplace de la función f(t).
- ilt(g(s),s,t)
Es el comando a utilizar para la realizar la transformada de Laplace inversa de la función g(s).
Algunos ejemplos del uso del comando laplace. Los tres últimos muestran propiedades generales:
- laplace(1,t,s);
- laplace(t^2,t,s);
- assume(n+1>0)$ laplace(t^n,t,s);
- laplace(cos(a*t),t,s);
Los siguientes muestran propiedades generales de la transformada de Laplace
Es un operador lineal
- laplace(a*f(t)+b*g(t),t,s);
Conportamiento respecto a la derivada
- laplace('diff(f(t),t),t,s);
- laplace('diff(f(t),t,2),t,s);
Para otras propiedades de la transformada de Laplace, así como la tabla de las transformadas de Laplace más comunes, deben consultarse bibliografía específica. En Wikipedia se aborda la cuestión.
Una ilustración de la transformada y su inversa (observe el cambio de orden entre t y s):
- f(t):=t^2;
F: laplace(t^2,t,s);
- ilt(F,s,t);
La transformada de Laplace es un instrumento útil para abordar la solución de ecuaciones diferenciales.
La técnica consiste en aplicar la transformada de Laplace a ambos miembros de la ecuación diferencial, lo cual da origen a una ecuación algebraica. Si la ecuación algebraica es posible resolverla, haciendo uso del teorema de Lerch, podemos obtener también la solución de la ecuación diferencial utilizando la inversa de la transformada de Laplace.
Vamos a resolver la ecuación diferencial de orden dos correspondiente al oscilador armónico:
diff(x(t),t,2)+x(t)=0, con condiciones iniciales x(0)=0, x'(0)=1 utilizando la técnica de la transformada de Laplace.
- E1 : 'diff(x(t),t,2)+x(t)=0;
- /* aplicamos la transformada de Laplace*/
E2 : laplace(E1,t,s);
- /* aplicamos CONDICIONES INICIALES; obsérvese la forma de hacerlo */
E3 : ev(E2, x(0)=0, at('diff(x(t),t),t=0)=1);
- /* resolvemos la ecuación algebraica obtenida, con incógnita laplace(x(t),t,s) */
E4 : solve(E3,laplace(x(t),t,s));
- /* deshacemos la lista */
E5 : E4[1];
- /* finalmente, la inversa de transformada de Laplace nos da la solución */
ilt(E5,s,t);
- Las operaciones para encontrar solución de esa ecuación diferencial de orden 2 con coeficientes constantes, que es similar a la del oscilador armónico, se muestran todas ellas en la consola

kill(all)$
print("La ecuación diferencial")$
ED : 'diff(x(t),t,2)-10* 'diff(x(t),t) + 9* x(t)=5*t;
print("su transformada de Laplace + condiciones iniciales")$
laplace(ED,t,s);
ev(%,x(0)=-1, at('diff(x(t),t),t=0)=2);
solve(%,laplace(x(t),t,s));
first(%);
ilt(%,s,t);
El comando desolve utiliza internamente la transformada de Laplace para resolver algunas ecuaciones diferencial o un sistema de ecuaciones diferenciales ordinarias con condiciones iniciales en el origen.
- desolve(ED,variable)
desolve([ED_1,ED_2...,ED_n],[variable_1,variable_2,...,variable_n])
Las ecuaciones diferenciales (ED, ED_1,ED_2...,ED_n deben ser escritas haciendo aparecer la variable (que por comodidad llamaremos t) de forma explícita; es decir, no basta con poner f como ocurre con ode2,
es necesario escribir f(t).
Si las condiciones iniciales en t=0 son conocidas, deben ser suministradas antes de llamar a desolve haciendo uso previo de uno o varios comandos
atvalue(expresión, t=0 , valor)
Si el comando no puede resolver la ecuación diferencial lineal, o el sistema de ecuaciones diferenciales lineales, devuelve false.
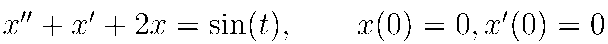
Lo hacemos por etapas para facilitar su comprensión:
kill(all)$
EC1: 'diff(x(t),t,2)+'diff(x(t),t) +2* x(t) = sin(t);- print("Establecemos condiciones iniciales en t=0")$
atvalue(x(t), t=0, 0)$
atvalue( 'diff(x(t),t), t=0, 0)$
- print("Obtenemos la solución con desolve")$ desolve( EC1, x(t));
- Ahora un sistema lineal de ecuaciones con las condiciones iniciales: f(0)=1, g'(0)=a; igualmente por etapas
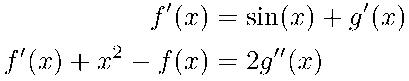
- kill(all)$
- EC1:'diff(f(x),x)=sin(x)+'diff(g(x),x); EC2:'diff(f(x),x)+x^2-f(x)=2*'diff(g(x),x,2);
- atvalue(f(x),x=0,1); atvalue('diff(g(x),x),x=0,a);
- SOL : desolve([EC1,EC2],[f(x),g(x)])
- SOL[1];
SOL[2];
- Los resultados en la consola
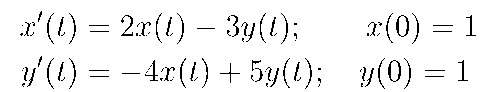
kill(all)$
print("Escribimos las ecuaciones y les ponemos nombre")$
EC1:'diff(x(t),t)=2*x(t)-3*y(t);
EC2:'diff(y(t),t)=-4*x(t)+5*y(t);
print("Establecemos condiciones iniciales en t=0
antes de utilizar desolve")$
atvalue(x(t),t=0,1); atvalue(y(t),t=0,1);
SOL : desolve([EC1,EC2],[x(t),y(t)])$
print("Separamos las dos soluciones x(t), y(t)")$
SOL[1];
SOL[2];

Métodos numéricos
Cuando los métodos para encontrar usa solución explícita de una ODE fracasan, es posible todavía acudir a métodos numéricos que permiten obtener valores aproximados y dibujar la curva solución
El paquete "dynamics"
El paquete "dynamics" proporciona funciones para representar gráficamente sistemas dinámicos discretos, fractales y soluciones numéricas de ODE mediante Runge-Kutta de orden 4.
load(dynamics);
Centrándonos en las ecuaciones diferenciales, el comando para Runge-Kutta que implementa el paquete es:
rk(Fórmula,Variable, Valor,Dominio)
Donde Fórmula corresponde a una expresión del tipo f(x,t) supuesto que la ODE se expresa en la forma
x'=f(x,t), donde x sería la Variable dependiente y t la independiente;
Valor es el de la variable x correspondiente al ValorInicial de la variable t; y Dominio es una lista del tipo [t,ValorInicial,ValorFinal,Incrementos] que establece el rango de variabilidad de t y el nivel de discretización.
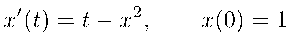
El comando ode2 fracasa. Gráfica de la solución por métodos numéricos.
puntos : rk(t-x^2,x,1,[t,0,20,0.1])$ /* puntos por los que pasa la curva solución */
plot2d([discrete,puntos]);
- Una órbita periódica de la ecuación de van der Pol
a:7; /* Ir incrementando el valor de a: 8,9,...*/
vdp1 : rk([y,-x-(x^2-1)*y],[x,y],[1,1],[t,0,a,0.1])$
vdpp1: makelist([vdp1[k][2],vdp1[k][3]],k,1,10*a)$
plot2d([discrete,vdpp1]);
- Si rk encuentra que una de las componentes alcanza valores demasiado grandes (en valor absoluto) la
iteración se detendrá como ocurre aquí:
rk(y^2,y,1,[t,0,10,0.1])$
puntos : rk(y^2,y,1,[t,0,10,0.01])$
print("se detiene en ",length(puntos))$
El paquete "plotdf"
El paquete "plotdf" permite crear gráficos del campo de direcciones de una ODE unidimensional y de campos de vectores en el plano, dando la posibilidad adicional de elegir soluciones u órbitas
de forma interactiva. El método numérico de integración es el de Adams-Moulton pero es posible optar por Runge-Kutta de orden 4 con paso de integración autoadaptativo
load(plotdf)$
La herramienta es muy útil para dibujar el campo de direcciones de una ecuación diferencial y visualizar el comportamiento de las soluciones. No entraremos aquí en los detalles, que el lector interesado puede encontrar en el manual de Maxima, únicamente ilustraremos con algunos ejemplos el uso del comando plotdf que el paquete implementa
- Una ecuación diferencial, tal como y'=x-y^2, corresponde al problema de encontrar una función
y(x) que verifique la ecuación diferencial anterior. La información que proporciona
la ecuación es que para cada (x,y) del plano es posible conocer la dirección
de la curva solución en dicho punto. El comando "plotdf" dibuja ese campo de direcciones; y pinchando en un punto se obtiene la órbita para el punto.
plotdf(x-y^2,[x,y],[x,-1,5],[y,-5,5])$
- Para la ecuación diferencial y'= exp(-x) +y mostramos el campo de direcciones y la curva solución que pasa por (2,-0.1). Pinchando con el ratón en cualquier punto se muestra dinámicamente la correspondiente curva solución pasando por dicho punto.
plotdf(exp(-x)+y,[trajectory_at,2,-0.1])$
- La ecuación de Duffing m*x"+c*x'+k*x+b*x^3 = 0 donde los coeficientes son parámetros, es una ecuación de segundo orden, que puede ser transformado en un sistema de ecuaciones de primer orden haciendo x'=y lo que permite hacer uso de
plotdf
plotdf([y,-(k*x + c*y + b*x^3)/m],
[parameters,"k=-1,m=1.0,c=0,b=1"],
[sliders,"k=-2:2,m=-1:1"],[tstep,0.1])$
- Van der Pol en el plano de Liénard
plotdf([y-(x^3/3-x),-x],[x,-5,5],[y,-5,5])$
- Este ejemplo, y el siguiente, utilizan parámetros
plotdf([e*(y-(x^3/3-x)),a-x],[x,-5,5],[y,-5,5],
[parameters,"a=0,e=1"],[sliders,"e=1:20,a:0:2"],[nsteps,500],[xfun,"x^3/3-x"])$
- plotdf([e*(y-(x^3/3-x)),a-x],[x,-3,3],[y,-3,3],
[parameters,"a=0.983,e=8"],[sliders,"a=0.982:0.984"],[nsteps,500],[xfun,"x^3/3-x"])$

 Ap_EcuacionesDiferenciales.wxmx
Ap_EcuacionesDiferenciales.wxmx