


En esta simulación vamos a tratar, desde el punto de vista cuántico, el problema de una partícula confinada en un Pozo de Potencial. A lo largo de la explicación detallaremos los pasos a seguir para llevar a cabo el estudio de la energía de la partícula en este curioso sistema. Así, tras explicar brevemente la situación general, procedemos a introducirnos en el estudio principal.
*' Como veremos más adelante, la cuántica no nos permite describir con precisión la posición de la partícula y trabajamos con probabilidades (un claro ejemplo de las consecuencias de esta característica es el llamado "efecto túnel" , ver abajo)

La magnitud a analizar en este problema es la energía de la
partícula (E) dentro del pozo. Pero, como hemos comentado antes, el estudio se
realizará desde el punto de vista cuántico, lo que implica romper con ciertos
conceptos procedentes de la mecánica clásica. El principal cambio a tener en
cuenta es el que afecta a la hora de determinar las magnitudes referentes a la
partícula, ya que analíticamente no podremos obtener un valor concreto para esa
magnitud, sino un espectro de valores y la probabilidad de encontrar cada uno de
ellos. Y es así como vamos a tratar la energía de esta partícula. Para hallar
estos valores debemos encontrar un tipo de funciones en concreto que sean
propias del operador correspondiente, es decir, funciones tales que al aplicarles el operador se
obtenga como resultado un valor multiplicando a la función misma. Las funciones de
estado de la partícula en el pozo siempre serán combinación lineal de estas
funciones propias, por lo que los valores de energía permitidos para dicha
partícula serán los propios de cada función.
correspondiente, es decir, funciones tales que al aplicarles el operador se
obtenga como resultado un valor multiplicando a la función misma. Las funciones de
estado de la partícula en el pozo siempre serán combinación lineal de estas
funciones propias, por lo que los valores de energía permitidos para dicha
partícula serán los propios de cada función.
Estas funciones (funciones de estado) son aquellas que aportan toda la información del sistema en concreto, además, mediante la "Densidad de probabilidad" (el módulo de la función al cuadrado: Ψ --> |Ψ|2). Así, |Ψ|2 nos permite hallar la probabilidad que hay de encontrar a la partícula en cierto intervalo, quedando esta definida como el área encerrada por |Ψ|2 y los extremos del intervalo. Es por esto que la integral de |Ψ|2 debe ser finita (y en concreto se debe normalizar para que valga 1).
De este modo debemos descubrir cuales son los autovalores pertenecientes a estas funciones propias del hamiltoniano, es decir, hallar los valores de energía posibles para esa partícula en la caja. Para ello necesitaríamos conocer esas funciones, y es aquí donde comienza el uso de los métodos de resolución matemática.
Para descubrir qué funciones de estado son las propias del hamiltoniano recurriremos a las propiedades y condiciones de contorno que deben cumplir. Estas condiciones vienen impuestas por la definición de función de estado que establece que ésta y su derivada deben ser continuas en todo el intervalo de definición. Además, para ser autofunciones de la energía deben cumplir la siguiente ecuación, que viene marcada por la definición de los operadores de la energía cinética y el potencial:
.gif)
Y en el caso de que el valor sea constante, llamaremos al operador "Energía":
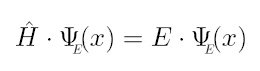
Como se puede observar, esta igualdad es una ecuación diferencial de segundo
grado, por lo que el programa utilizado es incapaz de resolverla analíticamente.
Para obtener una solución numérica aproximada recurrimos al
 método de
discretización
método de
discretización
 de la función que buscamos. Como podemos observar,
este método puede llegar a ser preciso pero no tanto como la solución analítica,
gracias a la cual obtenemos soluciones exactas del problema. A pesar de ello,
este método es bastante útil ya que obtenemos datos bien aproximados sin
necesidad de recurrir al cálculo simbólico que en algunos casos puede llegar a
ser tedioso y/o de complejidad extrema.
de la función que buscamos. Como podemos observar,
este método puede llegar a ser preciso pero no tanto como la solución analítica,
gracias a la cual obtenemos soluciones exactas del problema. A pesar de ello,
este método es bastante útil ya que obtenemos datos bien aproximados sin
necesidad de recurrir al cálculo simbólico que en algunos casos puede llegar a
ser tedioso y/o de complejidad extrema.

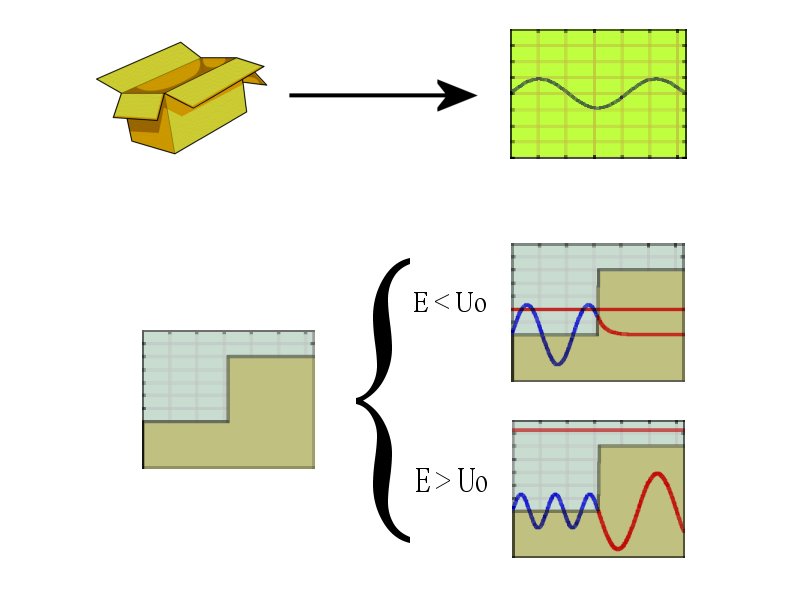
Como ya hemos comentado, esta situación se diferencia bastante de la partícula en una caja (como se muestra en la imagen inferior), ya que en este caso la partícula tiene el mismo potencial en cualquier zona de la caja, y es infinito en ambas paredes (que actúan de frontera). En la situación actual, podemos distinguir claramente dos casos: E<Uo y E>Uo (ver imagen). Siendo ambos diferentes del anterior.
| INDICACIONES |
| -Elija la "altura" del pozo (es decir, el valor de Uo); para ello introduzca el valor deseado en el campo numérico de la derecha y presione "return". |
| -Para poder obtener los valores propios de la energía vaya probando valores moviendo el deslizador (en el centro) hacia la derecha. Cuando observe que está cerca de un valor propio puede utilizar el campo numérico de la izquierda para una mayor precisión. |
| -Habremos hallado un valor de la autofunción cuando obtengamos en la Zona II una curva exponencial con límite 0 (para obtener un área finita). |
| -La barra marrón horizontal representa el valor de la Energía, pero su valor no se corresponde con el asignado por la gráfica ya que esta barra está en proporción con el pozo (el valor de E se muestra en el campo numérico). |
THE END Volver