Ecuación de Schrödinger: Pozo de potencial

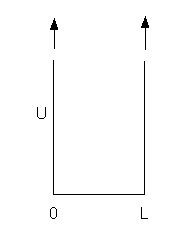
Partícula en un pozo de potencial de anchura L.

La ecuación de Schrödinger en una dimensión viene dada por:

(h/2∗π)²   d² f
- -----------   ------ 
      2m        dx²  		+ U(x) ∗ f(x) = E ∗ f(x)

Si tenemos en cuenta la expresión a la que se llega en el apartado Discretización de la ecuación de Schrödinger.

f [i+1] = (2.0 - Δ x² ∗ [ U(x) - E ]) ∗ f [i] - f [i-1];

Debemos especificar el valor de U(x) para iterar la expresión, en este caso queremos estudiar una partícula que se encuentra en un potencial que es infinito salvo en un espacio de amplitud L.
El potencial U(x) sera cero en el interior del pozo, 0 < x < L y fuera de él infinito por lo que la función de ondas debe valer cero en los extremos del mismo. En estas condiciones la ecuación de Scrödinger tiene solución analitica, son funciones armónicas dentro del pozo y los valores posibles de la energía vienen dados por:

E = n² 3.1416²

Donde se ha tomado como unidad de energía: h²/2m L²

Teniendo en cuenta este potencial la expresión a iterar nos queda:

f [i+1] = (2.0 - Δ x² ∗ E ]) ∗ f [i] - f [i-1];

Podemos obtener valores discretos de la función para cualquier energía; las energías para las que la función de onda se anule en ambos extermos del pozo será solución de nuestra ecuación puesto que cumple así las condiciones de contorno de nuestro problema especificadas por la función potencial.

Cálculo numérico.
Dando un valor para la energía E y el valor inicial para la función f [0] = 0 y un valor arbitrario, razonablemente pequeño, para el siguiente valor de la función por ejemplo f [1] = 0.1, vemos si la función se hace cero en L, cuando esto sea así ese valor de E es uno de los valores buscados para la energía.

En el siguiente enlace se puede ver un ejemplo de una Simulación realizada con la herramienta de autor EJS, en la que podemos modificar facilmente la energía y comprobar para qué valor esta se vuelve a hacer cero.