Manualico de Maxima

El paquete draw de Mario Rodríguez Riotorto, ofrece nuevas posibilidades de grafismo a las implementadas en el núcleo de Maxima; en particular permite dibujar, sin necesidad de paquetes adicionales, gráficos 2D en implícitas o gráficos animados.

En el paquete draw se implementan los comandos draw2d y draw3d con el mismo propósito que los comandos plot2d y plot3d incorporados en el núcleo de Maxima. Y aunque sólo funciona de forma completa con Gnuplot, representa una interfaz más rica para que Maxima se relacione con Gnuplot. Aquí nos limitaremos a hacer una introducción al paquete indicando los comandos y parámetros básicos. Más información en: Saber más

Para disponer de los nuevos comandos, en versiones antiguas de Maxima, es necesario cargar el paquete de forma explícita mediante

También es posible (y aconsejable) configurar Maxima para que realice de forma automatizada la carga del paquete.
Para ello basta incluir en el archivo de configuración maxima-init.mac una línea con la instrucción load(draw);
Dicho archivo de configuración (en GNU/Linux) está situado en la carpeta correspondiente al usuario /home/usuario/.maxima/maxima-init.mac

La misma filosofía es aplicable a otros paquetes que usted use de forma habitual.

También colegas que usan Mac han necesitado aplicarla incorporando al archivo maxima-init.mac una línea con la instrucción
gnuplot_command: "/opt/local/bin/gnuplot";
para poder visualizar los gráficos generados por Maxima.

Gráficos 2D con el paquete draw

El comando draw2d es capaz de gestionar, uno o varios gráficos simultáneamente, que pueden ser de tipos diferentes (fórmulas en explícitas, en implícitas, en paramétricas, en polares...) cada uno con sus propios parámetros y opciones (que se precisan antes de declarar la figura); también existen opciones globales que afectan a todos los elementos (por ejemplo, el título del conjunto) y que es conveniente (pero no imprescindible) colocar al principio.

El comando utiliza una sintaxis estructuralmente clara que podemos esquematizar mediante:

draw2d(Opciones globales,
Opciones,
Tipo del gráfico(Parámetros),
Opciones,
Tipo del gráfico(Parámetros),
...);

Vamos a utilizar ese esquema para listar, en un único comando, todos los tipos disponibles, con sus correspondientes parámetros, y dejaremos para la sección Opciones una lista detallada de las posibilidades, si bien iremos introduciendo en los ejemplos buena parte de ellas de forma no ordenada. Hay opciones globales y otras locales; estas últimas tienen efectos sobre todo el código posterior, hasta que sean cambiadas por un nuevo valor.

draw2d(Opciones globales,
Opciones,
explicit(fórmula, variable, valor_inicial, valor_final),
Opciones,
parametric(fórmulas, variable1, valor_inicial, valor_final,variable2, valor_inicial, valor_final),
Opciones,
implicit(fórmula, variable1, valor_inicial, valor_final,variable2, valor_inicial, valor_final),
Opciones,
polar(fórmula, variable, valor_inicial, valor_final),
Opciones,
points([[x1,y1],[x2,y2],...]),
Lista de puntos Opciones,
vector([x,y],[incremento_x,incremento_y]),
Opciones,
polygon([x1,y1],[x2,y2],...),
Opciones,
triangle([x1,y1],[x2,y2],[x3,y3]),
Opciones,
rectangle([x1,y1],[x3,y3]),
Opciones,
ellipse(x_centro,y_centro,x_semieje,y_semieje,ángulo_inicio,ángulo_amplitud),
Opciones,
bars([x1,y1,ancho1],[x2,y2,ancho2]...[xn,yn,anchon]) )$

Los nombres de los tipos de gráficos y sus correspondientes parámetros en la lista precedente resultan "autoexplicativos", aunque más abajo pondremos una colección de ejemplos del funcionamiento del comando draw2d incorporando algunas Opciones locales y globales. Y aunque hay una sección específica introducimos ya algunas de uso frecuente.

Ejemplos de gráficos con draw2d

/* Un ejemplo muy básico de curva con ecuación explícita */
draw2d( explicit(cos(x),x,0,%pi/2) )$
/* Dos curvas juntas de colores y dominios diferentes */
draw2d( color=blue, /* no es necesario definirlo es color por defecto mientras no se cambie */ explicit(cos(x),x,0,%pi/2), color=red, explicit(x,x,0,1) )$
/* Curvas juntas de diferentes colores y tipo de ecuación. La sintaxis es más homogenea que en plot2d */
draw2d( color=blue, parametric(cos(t),sin(t),t,0,2*%pi), color=green, implicit(x^2+y^2=9,x,-3,3,y,-3,3), color=black, polar(2,t,0,2*%pi), color=red, polar(1+t*0.3,t,0,3*%pi))$
/* Varias curvas con título global y con colores y leyendas personalizadas */
draw2d( terminal = wxt, /* terminal recomendado */ title = "Varios tipos, colores y leyendas", /* Título global */ nticks = 200, /* densidad de los puntos */ xrange=[-4,4], /* prefijar rango visible en el eje X */ color=blue, line_width = 3, /* grosor de línea */ key="circunferencia en paramétricas", /* leyenda identificativa de la gráfica siguiente */ parametric(cos(t),sin(t),t,0,2*%pi), color=green, key="circunferencia en implícitas", /* las tildes requieren terminal = wxt */ implicit(x^2+y^2=9,x,-3,3,y,-3,3), color=black, key="circunferencia en polares", polar(2,t,0,2*%pi), color=red, key="espiral en polares", polar(1+t*0.3,t,0,3*%pi))$
/* Pintar puntos y unirlos con rectas */
draw2d( terminal = wxt, point_type=circle, /* apariencia del punto: OTROS filled_circle, square, filled_square, VER Opciones más abajo */ point_size=2, /* tamaño del punto */ points_joined=true, /* unir puntos con rectas */ color=blue, points( [[0,0],[1,1],[0,2],[0.5,1]]) )$
/* Controlando la ubicación de las leyendas (key) correspondientes a las líneas */
draw2d( key_pos=top_left, key = "Puntitos en trazado aleatorio", points_joined = true, /* pruebe: cambie true por impulses */ points(makelist([random(20),random(50)],k,1,10)), point_type = filled_down_triangle, point_size = 1, key = "Puntos en camino aleatorio", color = red, points(makelist(k,k,1,20),makelist(random(30),k,1,20)) /* Dos listas con las coordenadas */ )$
/* Siguen dibujos de polygon, triangle y rectangle: borde y relleno */
draw2d( line_width=3, /* grosor del trazo, en lo que sigue */ polygon([[0,0],[1,1],[0,2],[3,1]]), color=skyblue, transparent=true, /* suprime relleno de fondo */ triangle([0,0],[1,0],[2,2]), transform=[x+1,y+2,x,y], /* desplazamiento */ border = false, /* suprimir el borde */ transparent = false, /* no suprimir relleno de fondo */ triangle([0,0],[1,0],[2,2]))$
draw2d( line_width=8, fill_color=yellow, /* establecer color relleno de fondo hasta que se cambie */ color=red, polygon([[0,0],[1,1],[0,2]]) )$
draw2d( line_width=6, color=red, fill_color=gray90, polygon([[0,0],[1,1],[0,2]]), line_width=4, color=blue, transparent=true, polygon([[0.6,0],[.8,0],[0.8,0.8],[0.6,0.8]]), color=green, transparent=false, fill_color=magenta, polygon([[0.6,1],[1,1],[1,1.5],[0.6,1.5]]) )$
draw2d( xrange= [-3,10], /* rango de valores en los ejes x y */ yrange= [-3,4.5], fill_color = yellow, transparent = false, line_width=6, line_type = solid, /* tipo de la línea */ rectangle([-2,-2],[8,-1]), transparent = true, line_type = dots, /* línea de puntos */ line_width = 1, rectangle([9,4],[2,-1.5]) )$
/* Dibujando vectores */
draw2d( xrange = [0,10], /* rango de valores en los ejes x y */ yrange = [0,7], vector([0,1],[5,5]), color= red, head_length = 1, /* longitud de la punta de flecha: por defecto es 2 */ line_width = 2, /* grosor de la línea */ head_both = true, /* flecha por ambos lados */ vector([2,1],[5,5]), color = green, head_length = 0.5, /* valores como éste y menores son adecuados */ head_both = false, line_width = 5, vector([4,1],[5,5]))$
/* Elipse: importancia de una escala uniforme */
draw2d(terminal=wxt, xrange=[-6,6], /* rango de valores en los ejes x y */ yrange=[0,3.5], /* suprímalos y experimente el efecto */ proportional_axes=xy, /* escala uniforme: suprima y experimente */ ellipse(0,0,6,3,20,150) )$
draw2d( terminal = wxt, title = "Gráfico de barras", /* las tildes requieren terminal=wxt */ fill_color=red, fill_density=0.1, /* densidad del color de fondo */ yrange=[0,7], /* el rango en x se autoajusta */ bars([0.5,3,0.5],[1,5,0.5],[1.5,6,0.5],[2,4,0.5],[2.5,3,0.5]));
/* Pintar la cuadrícula */
draw2d( terminal= wxt, proportional_axes=xy, title = "Pintar cuadrícula: 3 por cada unidad", grid = [3,3], /* cuadrícula y densidad de la misma */ explicit(sin(x),x,0,2*%pi))$
/* Colores y marcas en los ejes */

draw2d(terminal=wxt, title = "Ejes de coordenadas de color rojo (tipos diferentes). Marcas en los ejes", xaxis = true, yaxis = true, xaxis_color = red, yaxis_color = red, xaxis_type = solid, xtics = {0}, /* sólo esa marca en el eje X, si hay varias se separan con comas */ ytics = none, xlabel= "Una sóla marca de este eje", ylabel= "Sin marcas en este eje", line_width=3, explicit(x^3,x,-1,1))$
/* Regiones coloreadas delimitadas por curvas */
draw2d( filled_func = 0, /* rellena de color siendo y=0 la "frontera" */ explicit(sin(x),x,0,10) )$
draw2d( filled_func = x, explicit(1+x^2,x,0,2) )$
/* Dos funciones, puntos de corte y gráficas con marcas en los ejes: cuentas + dibujo */ f1: 2*x^2-5*x+4$ f2: -8*x^2-x+30$ print("Puntos de corte")$ solve(f1=f2); /* resolver el sistema */ print("Ahora sin las x")$ [x1,x2]: map('rhs, solve(f1=f2)); /* olvidar las x */ draw2d(terminal=wxt, title = "Parcela delimitada entre las curvas f_{1} y f_{2}: cuentas y dibujo", fill_color = grey, filled_func = f2, /* frontera para relleno siguiente función e intervalo */ explicit(f1,x,x1,x2), filled_func = false, /* ya no más rellenos */ xaxis = true, /* dibuja el eje x */ xtics_axis = true, /* y la escala en ese eje */ yaxis = true, line_width = 2, key = "f_{1}", /* leyenda de la función f1 con subíndice */ color = red, explicit(f1,x,-3,3), key = "f_{2}", /* observe como poner subíndices en key y title */ color = blue, explicit(f2,x,-3,3) );
/* Elegir la fuente con carácter global */
draw2d(terminal=wxt, color=black, line_width=4, explicit (1+x^2,x,-0.2,2), fill_color=yellow, filled_func=true, explicit (1+x^2,x,0,1), xrange= [-0.2,1.2], yrange=[0,2.3], font="Courier",font_size =15, label(["f",0.5,1.4]))$
/* Personalizar marcas en los ejes en coordenadas concretas */
draw2d(terminal=wxt, title="Semielipse", proportional_axes=xy, font="Courier",font_size =20, xtics ={["-a",-1],["a",1]}, /* marcas personalizadas en coordenadas del eje 0X */ ytics=false, /* no marcas en OY */ yrange=[0,0.7], color=orange, line_width=3, implicit(x^2+4*y^2=1,x,-1,1,y,0,1/2), color=black, label(["f",0,0.6]))$
/* Distribución normal */
load(distrib)$ /* cargamos una librería para estadística */ draw2d(terminal=wxt, title = "Probabilidad", grid = true, axis_top = false, /* suprime borde superior */ axis_right = false, /* suprime borde derecho */ filled_func = true, fill_color = "light-blue", key = "Pr( -1 < X < 0 )", explicit(pdf_normal(x,0,1),x,-1,0), key = "Pr( 1 < X <2 )", fill_color = "dark-blue", explicit(pdf_normal(x,0,1),x,1,2), filled_func = false, color = red, key = "Densidad N(0,1)", explicit(pdf_normal(x,0,1),x,-3,3) )$
/* Un imagen con varios ingredientes y opciones */

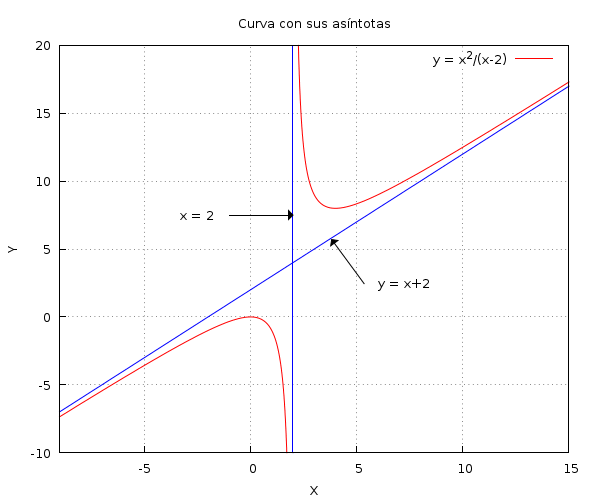
draw2d( terminal = wxt, title = "Curva con sus asíntotas", grid = true, /* incluir cuadrícula */ yrange = [-10,20], key = "y = x^2/(x-2)", color = red, explicit(x^2/(x-2),x,-9,15), key = "", /* sin nombres en lo sucesivo */ color = blue, explicit(x+2,x,-9,15), nticks = 70, /* densidad de puntos */ parametric(2,t,t,-10,20), head_length = 0.3, color = black, line_type = solid, vector([5.35,2.45],[-1.53,3.25]), vector([-1,7.5],[3,0]), label_alignment = left, /* alineación de la etiqueta */ label(["y = x+2",6,2.5]), /* etiqueta y coordenadas */ label_alignment = right, /* alineación diferente */ label(["x = 2",-1.7,7.5]) )$
/* Círculo y rectas */
draw2d( terminal=wxt, proportional_axes=xy, /* la misma escala en los ejes */ xaxis=false, /* no pinta eje OX */ yaxis=false, /* no pinta eje OY */ xtics=false, /* no pinta las marcas en OX */ ytics=false, /* no pinta las marcas en OY */ xlabel="", /* etiqueta eje X vacía */ ylabel="", /* etiqueta eje Y vacía */ border= false, /* no dibuja el borde de la elipse */ ellipse(0,0,1,1,0,360), color=black, point_size=0, /* no pinta los puntos */ points_joined=true, line_width=40, /* línea muy gruesa en las rectas */ points( [[-1/2,1/2], [1/2,-1/2]] ), points( [[-1/2,-1/2], [1/2, 1/2]] ) )$

Gráficos 3D con el paquete draw

Los gráficos 3D se obtienen haciendo uso del comando draw3d cuya sintaxis es similar a la del comando draw2d. únicamente varía el Tipo de gráfico y sus Parámetros.

draw3d(
Opciones,
explicit(fórmula, variable_1, valor_inicial_1, valor_final_1,variable_2, valor_inicial_2, valor_final_2) ),
/* z=f(x,y) */
Opciones,
implicit(fórmula, variable_1, valor_inicial_1, valor_final_1,variable_2, valor_inicial_2, valor_final_2,variable_3, valor_inicial_3, valor_final_3) ),
/* f(x,y,z)=C */
Opciones,
parametric_surface(fórmula_1,fórmula_2,fórmula_3, variable_1, valor_inicial_1, valor_final_1,variable_2, valor_inicial_2, valor_final_2) ),
/* x=f_1(u,v),y=f_2(u,v),z=f_3(u,v) */
Opciones,
spherical(fórmula, phi, valor_inicial_phi, valor_final_phi,theta, valor_inicial_theta, valor_final_theta) ),
/* radio=fórmula(u,v) u=phi varia entre 0 y 2*%pi ; v=theta varia entre 0 y %pi */
Opciones,
cylindrical(fórmula, r, valor_inicial_r, valor_final_r, phi, valor_inicial_phi, valor_final_phi) ),
/* z=fórmula(r,phi) * /
Opciones,
points([[x1,y1,z1],[x2,y2,z2],...]), (lo correspondiente para 2D)
Opciones,
points(Matriz de 3 columnas),
Opciones,
vector([x,y,z],[incremento_x,incremento_y,incremento_z]), (lo correspondiente para 2D)
Opciones,
triangle([x1,y1,z1],[x2,y2,z2],[x3,y3,z3]), (lo correspondiente para 2D)
Opciones,
quadrilateral([x1,y1,z1],[x2,y2,z2],[x3,y3,z3],[x4,y4,z4]), (lo correspondiente para 2D)
Opciones,
parametric(función_x, función_y, función_z, variable, mínimo_variable, máximo_variable),
Dibuja una curva alabeada (tridimensional)
Opciones,
tube(función_x, función_y, función_z, función_radio, variable_común, mínimo_variable, máximo_variable) )$
Dibuja un tubo siguiendo la curva tridimensional definida por función_x, función_y, función_z; el radio del tubo está definido mediante función_radio que usa la misma variable que las otras tres funciones.

Ejemplos de gráficos con draw3d

/* Un ejemplo sencillo */
draw3d( explicit(x^2-y^2,x,-1,1,y,-1,1) )$
/* Otro ejemplo con título */
draw3d( terminal=wxt, title = "Semiesfera superior en implícitas", /* al igual que en draw2d */ implicit(x^2+y^2+z^2=1, x,-1,1, y,-1, 1, z,0,1) )$
draw3d( terminal=wxt, title= "Semiesfera superior en paramétricas", /* las tildes pueden funcionar mal si no se usa el terminal wxt */ parametric_surface( cos(u)*cos(v),cos(u)*sin(v),sin(u), u, 0, %pi, v, 0, %pi) )$
/* Una apariencia mejorada */
draw3d( terminal=wxt, title = "Esfera completa en esféricas", enhanced3d=true, /* mejora la apariencia 3d */ colorbox=false, /* sin escala de profundidad */ spherical(1, t,0,2*%pi,s,0,%pi))$
/* Tonos grises, sin pintar los ejes y con escala uniforme en las 3 dimensiones */
draw3d( terminal=wxt, title = "Esfera completa en esféricas, tonos grises y escala homogénea", enhanced3d = true, palette = gray, /* tonos grises */ colorbox = false, axis_3d = false, /* elimina los ejes */ proportional_axes = xyz, /* escala uniforme en los tres ejes */ spherical(1, phi,0,2*%pi,theta,0,%pi) )$
/* Paraboloide */
draw3d( terminal = wxt, title = "Paraboloide en cilíndricas", enhanced3d=true, palette=[3,4,5], /* control en colores en enhanced3d */ colorbox = false, cylindrical(r^(1/2), r,0,1, phi,0,2*%pi));
draw3d( title = "Cilindro de altura 1 y radio 1", cylindrical(1, r,0,1, phi,0,2*%pi));
draw3d( terminal = wxt, title = "Cono en cilíndricas", cylindrical(r, r,0,1, phi,0,2*%pi));
/* Con curvas de nivel y parcialmente oculta */
draw3d( title = "Paraboloide con curvas de nivel", color=gray, contour_levels = 10, contour = both, surface_hide = true, explicit(x^2+2*y^2,x,-1,1,y,-1,1) )$
/* Control de etiquetas en los ejes y del ángulo de mira */
draw3d( title="Superficie de revolución en torno a 0X: IMPLíCITAS", terminal=wxt,enhanced3d=true, colorbox=false, axis_3d=false, xlabel="", /* elimina etiqueta del eje que se indica */ ylabel="", zlabel="", view=[105,4], /* ángulo de mira */ zaxis=true, implicit(y^2+z^2=x^4,x,0,1,y,-1,1,z,-1,1))$
/* Superficie de revolución en torno a 0X: PARAMÉTRICAS */
draw3d( title="Superficie de revolución en torno a 0X: PARAMÉTRICAS", terminal=wxt,enhanced3d=true, colorbox=false, axis_3d=false, xlabel="", ylabel="", zlabel="", view=[105,4], zaxis=true, palette=[6,7,8], parametric_surface(x,x^2*cos(t),x^2*sin(t),x,0,1,t,0,2*%pi))$
/* Camino tridimensional aleatorio mediante una matriz */
/* matriz aleatoria: 3 coordenadas 5 puntos */ M:apply(matrix,makelist(makelist(random(10.0),i,1,3),j,1,5)); draw3d( title = "Camino tridimensional aleatorio mediante una matriz", point_type=filled_diamant, /* otro tipo de punto */ point_size=2, color=blue, points_joined=true, points(M));
/* Vectores en el espacio 3D */
draw3d( title = "Vectores", head_length=0.05, /* longitud de la punta del vector */ color=red, vector([0,0,0],[1,1,1]), color=green, vector([0,0,0],[1,0,0]), head_both = true, /* vector con dos puntas */ color=blue, vector([1,0,0],[0,1,1]))$
/* Triángulo en el espacio 3D */
draw3d( terminal = wxt, title = "Triángulo", enhanced3d=true, color=green, triangle([0,0,0],[1,1,0],[2,2,2]))$
/* Triángulo en el espacio 3D con transformación */
draw3d( transform = [x+1,y^2,z+1,x,y,z], triangle([0,0,0],[1,1,0],[2,2,2]))$
/* Curva en 3D */
draw3d( terminal=wxt, title = "CURVA en 3D", color=royalblue, line_width=3, nticks=150, parametric(cos(t),sin(t),t+1,t,0,6*%pi))$
/* Tubo siguiendo una curva plana */
draw3d( terminal=wxt, title = "TUBO de grosor variable siguiendo curva plana", colorbox=false, enhanced3d = true, xu_grid = 50, tube(cos(a), a, 0, cos(a/10)^2, a,0,4*%pi) )$
/* Tubo siguiendo una curva plana: tapando los extremos */
draw3d( terminal=wxt, title = "TUBO de grosor fijo 1 y un extremo tapado", surface_hide = true, enhanced3d = true, colorbox=false, tube_extremes=[open,closed], /* tapar los extremos */ tube(a, a, a^2, 1, a, -2, 2) )$
/* Tubo de varios colores */
draw3d( terminal =wxt, enhanced3d = true, palette = [red, blue, yellow], /* control de colores */ xu_grid = 50, tube(cos(a), a, 0, 1, a, 0, 4*%pi) )$
/* Cilindro rodeando una esfera */
draw3d( terminal = wxt, title ="Sin ejes, sin leyendas, sin marcas,...", surface_hide = true, /* no dibuja las partes ocultas */ axis_3d = false, /* no dibuja ejes de coordenadas */ xtics = none, /* sin marcas en el eje X */ ytics = none, ztics = none, xlabel = "", /* sin leyenda en el eje X */ ylabel = "", zlabel = "", view = [70,77], /* punto de mira: usar ratón para decidir */ parametric_surface(cos(a)*cos(b), cos(b)*sin(a), sin(b), a,0,2*%pi, b,-%pi/2,%pi/2), color = cyan, /* color en 3D ordinario */ parametric_surface(1.01*cos(a), 1.01*sin(a), z, a,0,3/2*%pi, z,-1,1), xu_grid = 25, yv_grid = 5, parametric_surface(1.01*r*cos(a),1.01*r*sin(a),1,a,0,3/2*%pi,r,0,1), parametric_surface(1.01*r*cos(a),1.01*r*sin(a),-1,a,0,3/2*%pi,r,0,1))$
/* Plano cortando una campana de Gauss */
draw3d( terminal = wxt, key = "Gauss", color = blue, explicit(20*exp(-x^2-y^2)-10,x,-4,4,y,-4,4), yv_grid = 10, color = red, key = "Plano", explicit(x+y,x,-5,5,y,-5,5), surface_hide = true, view = [75,50] );
/* Dos toros */
draw3d( enhanced3d = sin(u)+cos(v), colorbox=false, axis_3d=false, zlabel="", ylabel="", palette = [8,4,3], dimensions = 100*[10,10], parametric_surface(cos(u)+.5*cos(u)*cos(v), sin(u)+.5*sin(u)*cos(v), .5*sin(v), u, -%pi, %pi, v, -%pi, %pi), parametric_surface(1+cos(u)+.5*cos(u)*cos(v), .5*sin(v), sin(u)+.5*sin(u)*cos(v), u, -%pi, %pi, v, -%pi, %pi)) $ draw_file(terminal = pdf, file_name="2toros")$
/* Plano tangente a una superficie. Conlleva cálculos previos incorporados */
kill(all)$ f(x,y):=3+x^2+y^2$ x0: 0.1$ y0: -0.7$ z0: f(x0,y0)$ jacobian([f(x,y)],[x,y])$ grad: ev(%,x=x0,y=y0)$ S: grad.[x, y]$ T: z0+grad.[x-x0, y-y0]$ addcol(grad,[-1])$ N:list_matrix_entries(%)$ a:2$ draw3d( title="Superficie y plano tangente f:R²→R", terminal = wxt, surface_hide = true, ztics='none, ytics='none, xtics='none, view=[75,70], explicit(f(x,y),x,-a,a,y,-a,a), color=green, explicit(T,x,-a,a,y,-a,a) )$

Conviene saber que si está usando wxMaxima como interfaz gráfico, existen los comandos wxdraw2d y wxdraw3d cuya sintaxis y funcionamiento coincide con el de los correspondientes draw2d y draw3d con la salvedad de que las imágenes, en lugar de mostrarse en una ventana independiente, quedan incrustadas en el propio fichero, como ocurre con las salidas no gráficas.

Opciones del paquete draw

El paquete draw introduce multitud de comandos para controlar las opciones de draw2d, draw3d y draw (no descrito en estas notas). Las que nos han resultado de uso más frecuente han ido apareciendo en los ejemplos anteriores, pero hay más.

Nos limitaremos a hacer una lista amplia de dichos opciones que pueden tener carácter global (como por ejemplo, title) o local (color para un objeto concreto).

es posible obtener una breve descripción y algunos ejemplos de uso para el correspondiente comando. En los ejemplos precedentes han aparecido algunas ilustraciones del uso de buena parte de las opciones que aparecen a continuación y que están resaltadas.

Globales

Afecta a todos los elementos, independientemente de su posición relativa en el código.

Locales

Afecta a los elementos que van detrás: la posición en el código es fundamental.

Guardar los gráficos para su reutilización

Como ya hemos indicado anteriormente, utilizar la opción global terminal=wxt permite, utilizando los menús de la ventana en que se muestra, guardar el gráfico que se está visualizando en formato png, pdf, svg para una posterior reutilización. Pero además existen otras posibilidades para guardar el gráfico que describimos ahora:

Gnuplot recibe de Maxima un fichero de texto plano que procesa para generar el gráfico que puede guardar en diferentes formatos (png, pdf...) como ya hemos señalado más arriba que son directamente utilizables por LaTeX y otros editores. Pero los números y textos que aparecen en los png, pdf... no coinciden, generalmente, con los que usa LaTeX, algo que incomoda a los usuarios LaTeX que necesitan incorporar las figuras en sus documentos. Afortunadamente Gnuplot es consciente del problema y es capaz de construir a partir del fichero en texto plano que recibe un nuevo fichero en texto plano y código tikz destinado específicamente a LaTeX, que puede ser personalizado a posteriori por usuarios LaTeX exigentes y habilidosos.

Tales ficheros en formato tikz se pueden conseguir utilizando la opción user_preamble que le permite al usuario escribir en el fichero de texto plano que Gnuplot recibe instrucciones personales destinadas a Gnuplot: una sola en cada línea.
Es algo que suelo utilizar. Y como ilustración podemos utilizar el ejemplo anterior ligeramente modificado

generando en este caso un fichero MiFigura.tikz que se guarda en la carpeta ("home") personal del usuario y que puede incorporar a un fichero .tex mediante \input{MiFigura.tikz}.
Desde la consola de Maxima y usando xMaxima he procesado el código anterior sin ningún problema; pero no lo he conseguido con wxMaxima a causa de un problema de permisos en la carpeta /tmp (pendiente de resolver).

En el preámbulo de dicho archivo para LaTeX debe aparecer la instrucción \usepackage{gnuplot-lua-tikz}.

Los usuarios de LaTeX entenderán inmediatamente las ventajas de poder editar y personalizar el fichero MiFigura.tikz, por ejemplo, para reescribir las fórmulas usando la sintaxis de LaTeX, para reescalar la figura sustituyendo, [gnuplot] por [gnuplot,scale=0.5], etc.

Con una estructura similar puede generarse un fichero MiFigura.pst en formato pstricks utilizando como terminal pstricks

Gráficos animados

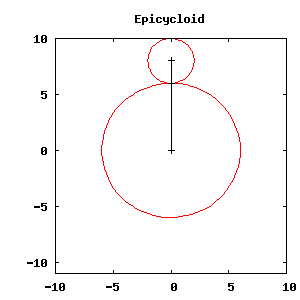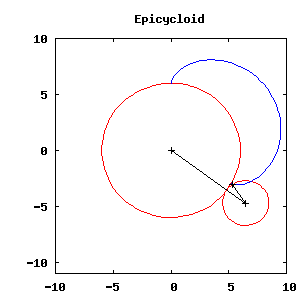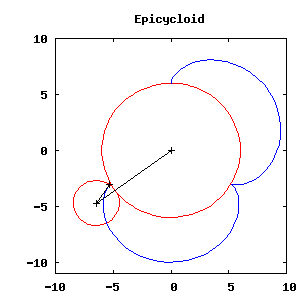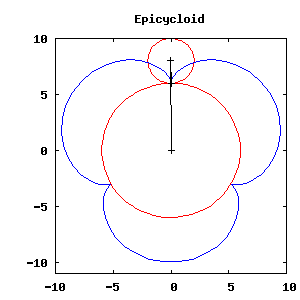
Esta es una figura animada realizada con Maxima y draw. Dentro del navegador de xMaxima no podrá ver la animación, pero sí podrá verla en un navegador estándar. El código para generar esta figura y otros ejemplos de gráficos animados puede encontrarlos em http://riotorto.users.sourceforge.net/Maxima/gnuplot/animations/index.html

Mostramos a continuación algunos gráficos animados elaborados usando wxMaxima y que deben ser abiertos con dicho interfaz. No los abra desde el navegador de xmaxima.

Gráficos con el paquete draw

Cargar el paquete draw: lo primero a hacer