Gráficos usando plot2d y plot3d
Maxima tiene la posibilidad, via programas externos, de producir gráficos de
funciones en 2 y 3 dimensiones. También puede producir gráficos a partir de una
tabla de puntos. Actualmente pueden utilizarse como programas externos
openmath, (identificado también como xmaxima),
gnuplot, mgnuplot y geomview.
La opción por defecto es
actualmente gnuplot siempre que esté disponible, que es muy rica en posibilidades y permite exportar los gráficos a diferentes formatos, en particular a tikz que resulta muy adecuado para su uso en LaTeX.
En estas notas nos limitaremos a las opciones que usamos más frecuentemente en la docencia. Véase al final de esta página la sección Saber más
 Gráficos 2D con Maxima básico
Gráficos 2D con Maxima básico
El comando para dibujar es plot2d y la sintaxis la vamos a ir
analizando progresivamente ilustrándola con ejemplos. Es posible
dibujar gráficas de funciones expresadas sea en coordenadas explícitas, paramétricas, implicitas y también utilizando una colección de puntos. Haciendo uso de la opción
gnuplot_preamble, con los parámetros adecuados, es posible dibujar también en polares (más abajo hay un ejemplo).
- plot2d( [expr_1, ..., expr_n], [variable,mínimo,máximo], opciones)
Permite dibujar una o varias funciones simultáneamente definidas en coordenadas explícitas. Todas con el mismo intervalo de la variable. Cuando sólo hay una función los corchetes [ ] pueden eludirse. La fórmula de la función aparece en el eje vertical cuando sólo hay una y cuando son varias aparecen en la esquina del rectángulo; en tal caso plot2d va cambiando automáticamente de color.
- plot2d( [parametric, x_expr, y_expr, t_rango],
opciones)
Como su nombre sugiere es el comando para dibujar curvas en coordenadas paraméticas utilizando la fórmulas para las variables x e y junto con el intervalo de variación del parámetro.
- implicit_plot( [expr_1, ..., expr_n], [x, min, max], [y, min, max])
Para dibujar una o varias curvas con ecuaciones en coordenadas implícitas. Y requiere un paquete adicional que sólo hay que cargar previamente, por una sola vez en la sesión,
mediante load(implicit_plot)$.
- plot2d( [discrete, lista_de_puntos], opciones)
Es el comando para dibujar una lista de puntos determinados por sus coordenadas, unidos formando una poligonal.
Comenzamos con algunos ejemplos que ilustran el funcionamiento, pero prescindimos por ahora de las opciones que, como su nombre sugiere, no son obligatorias.
- /* Tres curvas en la misma imagen */
plot2d([sin(x), x^2, cos(x)], [x,0,%pi/2])$
- /* Otra curva en explícitas */
plot2d(cos(x), [x,-%pi,%pi])$
- /* Las funciones se pueden definir antes y a trozos */
f(x):=x^3$
g(x):= if x< 0 then x^2 elseif x <1/2 then x$
plot2d( [f(x),g(x)],[x,-1,1] )$
Las funciones definidas a trozos permiten personalizar el dominio de las mismas, sin necesidad de que coincida
con el global.
Experimente con definiciones como las siguientes:
g(x):= if x< 0 then x^2 else x$
g(x):= if x< 0 then x^2$
- /* Circunferencia en paramétricas */
plot2d( [parametric,cos(t),sin(t),[t,-%pi,%pi]])$
- /* Una curva en implícitas */
load(implicit_plot)$
implicit_plot(x^3-2*x*y+y^3, [x,-3,3], [y,-3,3])$
- /* Colección de puntos unidos por rectas */
plot2d([discrete, [ [10,.6], [20,.9], [30,1.1], [40,1.3], [50,1.4] ] ])$
- /* Cuatro funciones de tipos diferentes */
f(x):=-x^3$
g(x):= if x< 0 then x^2$
plot2d( [ f, g, [parametric, cos(t), sin(t) , [t,%pi/2,2*%pi]],
[discrete, create_list( [1/n,-1/2+n/(n+1)], n,1,5 )] ],
[x,-1,1] )$
A continuación se ilustran de algunas de las opciones de uso más frecuente.
1) Poner título a la imagen; o fijar el rango de valores de un eje, o de los dos;
2) Personalizar las etiquetas en los ejes;
3) Personalizar las leyendas de las las funciones;
4) Estilo de los puntos en gráficos discretos (y continuos).
Algunas de las opciones son específicas para ese tipo de comando, pero otras sirven para todos los tipos. Es fácil distinguirlas.
- /* Título e intervalos OX y OY independientemente del dominio de las x */
plot2d([sin(x), x^2], [x,-%pi,%pi],
[ title, "Dos funciones fijando el rango en los ejes"],
[x,-3.5, 3.5], [y,-1.2, 1.2])$
- /* Personalizar etiquetas de los ejes */
plot2d( log(x), [x,1, 10],
[ xlabel,"Eje OX"], [ylabel,"Eje OY"] )$
- /* Personalizar leyenda de las funciones */
f(x):=x^3$
g(x):= if x < 0 then x^2 elseif x < 1/2 then x$
plot2d( [f(x),g(x)],[x,-1,1],
[ legend, "f(x)", "g(x)" ] )$
Comparar con un resultado anterior
- /* Puntos en lugar de poligonales */
a[1]:2$ a[n]:= 1/(3 -a[n-1])$
plot2d([discrete, create_list([n,a[n]],n,1,10)],
[ style, points],
[xlabel,"n"], [ylabel,"a[n]"])$
plot2d([discrete, [ [1,2], [2,5],[3, 1] ] ], [y, 0,6],
[ style, [points,4]],
[xlabel,"base"],
[ylabel,"altura"])$
- /* Nivel de densidad de los puntos */
plot2d(entier(x),[x,-2.5,2.5],
[ nticks,100],
[legend,"Parte entera"], [ylabel, ""])$
Cambiando en el estilo de los puntos el resultado es mejor
plot2d(entier(x),[x,-2.5,2.5],
[nticks,100], [legend,"Parte entera"], [ylabel, ""],
[ style, [points,2]])$
- /* Circunferencia en paramétricas sin autoescalar*/
plot2d( [parametric,cos(t),sin(t),[t,-%pi,%pi]],
[same_xy])$
La utilización de coordenadas polares requiere hacer uso del comando gnuplot_preamble que también permite personalizar la posición de las leyendas de los gráficos, o enviar código directo a Gnuplot (lo cual requiere conocer el lenguaje que Gnuplot utiliza).
-
/* Una misma fórmula produce resultados diferentes utilizando las opciones */
plot2d( 3*cos (2*t),[t,-%pi,%pi]);
plot2d( 3*cos (2*t),[t,-%pi,%pi],
[ gnuplot_preamble,"set polar"]);
- /* Tres gráficas con leyendas y posición personalizada */
plot2d( [sin(x),cos(x), [discrete,[[0,0],[%pi,-1]]]], [x,-%pi,%pi],
[legend,"seno","coseno","recta"], /* leyendas */
[gnuplot_preamble,"set key top left"])$
 Gráficos 3D con Maxima básico
Gráficos 3D con Maxima básico
Las superficies pueden venir dadas usando: coordenadas cartesianas,
coordenadas cilíndricas, esféricas, o bien de forma paramétrica.
- plot3d(expresión, [variable_x mínimo, máximo], [variable_y mínimo, máximo], opciones)
La expresión es del tipo f(x,y) y corresponde a z=f(x,y) para coordenadas cartesianas
- plot3d ([expresión_1,expresión_2,...expresión_n], [variable_x mínimo, máximo], [variable_y mínimo, máximo], opciones)
Como la precedente salvo que dibuja varias superficies de forma simultánea.
- plot3d ([x_expresión, y_expresión, z_expresión],
u_rango, v_rango, opciones)
Las expresiones son del tipo f1(u,v), f2(u,v), f3(u,v) y corresponden a coordenadas paramétricas dadas por x=f1(u,v), y=f2(u,v), z=f3(u,v)
Primeros ejemplos
- /* La fórmula dependiendo del formato elegido puede o no mostrarse */
plot3d(-x^2 + y^2, [x, -3, 3], [y,-2,2],
[legend, false]
)$
- plot3d(-x^2 + y^2, [x,-3, 3], [y, -2, 2],
[plot_format, xmaxima])$
- /* geomview sólo funciona en GNU-Linux y ha de estar instalado */
plot3d(-x^2 + y^2, [x, -3, 3], [y, -2, 2],
[plot_format, geomview])$
- En el formato gnuplot
(wxWidgets) es posible guardar, desde los menús el gráfico tal y como se está visualizando en formato png, pdf, svg.
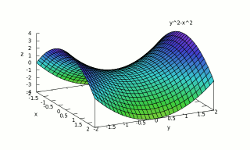
Es posible mover la superficie
usando el ratón o las flechas de los cursores.
Con el botón central del ratón se
cambian las escalas en los ejes.
Pulsando la tecla b se pinta o despinta la
caja.
Con la tecla g se quita y pone la rejilla de coordenadas (también puede
hacerse desde el menú).
-
En el formato xmaxima (openmath) pulsando el botón izquierdo del ratón puede
girarse el gráfico. Con el botón derecho se desplaza. Desde los menús es posible hacer zoom.
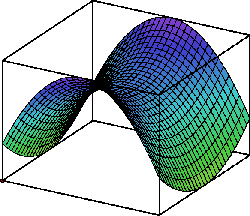
También es posible guardar el gráfico en la posición elegida
(plot3d) mediante una captura de pantalla implementada en los menús en formato
postscript.
- En el caso del formato
geomviev (que funciona sólo en GNU-Linux/Unix y que hay que instalarlo de forma
independiente de Maxima) puede conseguirse que el gráfico gire continuamente
tras darle un impulso inicial.

Más ejemplos:
- /* Una superficie con fórmulas parámetricas */
x1_expr:cos(v)*(10.0+6*cos(u))$
x2_expr: sin(v)*(10.0+6*cos(u))$
x3_expr: -6*sin(u)$
plot3d ([x1_expr, x2_expr, x3_expr], [u, -%pi, %pi],[v, -%pi, %pi],
[grid,60, 60],[legend, false],
[plot_format, gnuplot] )$
- /* Una superficie con fórmula cartesiana */
plot3d([-x^2+y^2,[x,-2,2],[y,-2,2]]);
- /* Dos superficies juntas, con leyendas ocultas */
plot3d([-x^2+y^2, 4*sin((x^2+y^2))/(x^2+y^2),[x,-2,2],[y,-2,2]],[legend, false] )$
- /* Lo mismo con el formato xmaxima, que tiene otra apariencia */
plot3d([-x^2+y^2, 4*sin((x^2+y^2))/(x^2+y^2),[x,-2,2],[y,-2,2]],
[plot_format, xmaxima]);
Cuando se utiliza más de una superficie, gnuplot, por defecto, emplea la misma paleta de colores en
todas ellas (también ocurre así con geomview). En cambio el formato xmaxima emplea una
paleta de color diferente para cada uno de ellos lo cual facilita la
identificación de las superficies.

Cilíndricas y esféricas
Este tipo de coordenadas también pueden ser empleadas en plot3d utilizando respectivamente:
[ transform_xy, polar_to_xy ]
[ transform_xy, spherical_to_xyz ]
En el primer caso se interpretan las dos variables independientes como polares, transformándolas luego a coordenadas cartesianas.
En el segundo caso se interpretarán las variables independientes como esféricas, transformándolas luego a coordenadas cartesianas.
Ejemplos:
- /* Un cono (lineal) de revolución */
plot3d(r,[r, 0, 1],[t, 0, 2*%pi],
[ transform_xy, polar_to_xy],[legend,false])$
- /* Un paraboloide (cuadrático) de revolución (no cerrado) */
plot3d(r^2,[r, 0, 1],[t, 0.4*%pi, 2*%pi],
[ transform_xy, polar_to_xy],[legend,false]);
- /* La esfera de radio 2 en esféricas */
/* el orden de los ángulos debe ser el indicado */
plot3d (2,[theta, -%pi/2, %pi/2],[phi, 0, 2*%pi],
[ transform_xy,spherical_to_xyz],[plot_format,xmaxima]);
- /* La semiesfera de radio 2 en esféricas */
plot3d(2,[theta, 0, %pi/2],[phi, 0, 2*%pi],[legend,false],
[ transform_xy,spherical_to_xyz]);
Conviene también saber que si se está utilizando wxMaxima como interfaz gráfico de trabajo existen
los comandos wxplot2d y wxplot3d cuya sintaxis y funcionamiento coincide con el de los correspondientes plot2d y plot3d salvo que las imágenes, en lugar de mostrarse en una
ventana independiente, quedan incrustadas en el propio fichero.
 Opciones
Opciones
En este apartado indicaremos como controlar mediante el argumento
opciones que figura en la sintaxis de plot2d y plot3d, y que no es
obligatorio, determinados aspectos del gráfico que modifican el comportamiento
obtenido por defecto. Ya hemos utilizado en los ejemplos precedentes alguna de las opciones disponibles.
Hay aspectos que están relacionados con la apariencia (como colores,
leyendas, títulos, densidad de puntos) y otros que tienen que ver el formato de
salida (como el tipo de programa que lo visualizará, si se guardará o no en un
fichero y en su caso cual será el formato gráfico utilizado). Estos dos aspectos
tienen una cierta autonomía, pero no son completamente independientes y el
primero de ellos está condicionado, con frecuencia, por el segundo.
índice de opciones
Opciones comunes a todos
los formatos gráficos
Opciones específicas para
formatos de Gnuplot
Maxima dibuja de acuerdo con una lista de opciones o parámetros que controlan
su comportamiento.
El valor actual de las opciones se obtiene ejecutando el comando
set_plot_option();
Pero el comando sirve también para una vez conocidos los valores de las diferentes opciones ejecutarlo de nuevo, indicando dentro del paréntesis, con sus respectivos corchetes y separados entre sí por comas, los nuevos valores que se desean asignar a dichas opciones. Tales valores se aplican a todos los gráficos mientras no sean cambiados durante la sesión.
También es posible incluir en el argumento de cada comando plot2d o
plot3d las opciones deseadas (con sus respectivos corchetes y separadas
entre sí por comas) en cuyo caso tales opciones sólo tendrán efecto en ese gráfico.
 Opciones comunes
Opciones comunes
Maxima puede utilizar
diferentes programas gráficos para dibujar; en este apartado se describen las
opciones comunes para todos los formatos gráficos que conoce. Posteriormente se
van detallando las nuevas opciones específicas para los formatos gnuplot (que es
el que tiene mayores posibilidades) y PS (muy elemental)
- [plot_format, Formato de salida ] Identifica
el Formato de salida en el que el gráfico será guardado y
(generalmente) Maxima realizará una llamada al programa correspondiente para
mostrar el gráfico. Cada formato de salida tiene una posibilidades diferentes y
por tanto los parámetros de dibujo que cada uno admite también.
Los valores posibles de Formato de salida son actualmente:
- gnuplot Utiliza el programa de dibujo Gnuplot
(que se gestiona en línea de comando) de uso muy extendido. Maxima requiere que esté instalado. Dependiendo del sistema operativo, la instalación de Maxima puede, o no, conllevar la instalación automatizada de Gnuplot.
Con este formato se
genera automáticamente un fichero maxout.gnuplot con un preámbulo
que contiene instrucciones en el lenguaje propio de Gnuplot y una tabla de
puntos. Este archivo, y otros similares que irán apareciendo más abajo, se
guarda, segn el sistema operativo en el directorio home (Documents and Settings) del
usuario. Internamente Maxima llama al programa gnuplot para que lea e interprete
este fichero (algo que corresponde a la instrucción load "maxout.gnuplot" de
Gnuplot). En el caso de MS-Windows puede ser necesario cerrar previamente el
gráfico actual antes de poder mostrar otro, lo cual resulta un incomodidad.
- gnuplot_pipes Es una variante de la
anterior usada por defecto en las plataformas distintas a MS-Windows. La
comunicación con Gnuplot se realiza a través de una tubería del sistema y en
lugar de maxout.gnuplot se genera un fichero
maxout.gnuplot_pipes
que contiene únicamente las coordenadas de los puntos del gráfico que Gnuplot se
encarga de dibujar.
- mgnuplot es una variante de
gnuplot, la diferencia es que muestra una ventana desde la que es posible
cambiar el punto de mira en gráficos tridimensionales y recuperar y modificar
los parámetros de configuración que gnuplot utiliza (escribir en la pantalla
Edit el código y pulsar Enter). En cuanto a visualización interactiva tiene
prestaciones similares a openmath, pero la información se guarda en dos
ficheros:
maxout.mgnuplot que contiene la tabla de puntos y
gnuoptionxx que es el que lee gnuplot y que contiene los parámetros
de configuración de gnuplot, de forma independiente, lo cual facilita la acción
sobre los mismos si se conocen los comandos de gnuplot. De hecho, a través de la
ventana Edit pueden ir cambiándose los parámetros, comprobando interactivamente
el efecto y guardar dichos parámetros en un fichero gnuplot.out que
se convierte así en un sustituto potencial de gnuoptionxx. Para poder realizar
esas operaciones interactivas es necesario tener instalado el intérprete wish
porque mgnuplot es un programita realizado en lenguaje tcl tk. En Linux el
intérprete wish suele estar instalado, no así en MS-Windows, pero también está
disponible bajo licencia GPL.
- openmath identificado también como xmaxima. Formato creado por Scherlter. Muy útil para la visualización de gráficos porque
permite desplazarlos (botón derecho del ratón), hacer zoom (pinchando donde
están las coordenadas), girar los tridimensionales (botón izquierdo del ratón) y
más cosas, entre otras guardarlo en formato postscript (no es muy fino en este
tema y genera ficheros muy grandes, por lo que resulta poco aconsejable). Los
gráficos pueden aparecer insertados dentro de xmaxima o en una ventana
independiente (que es lo aconsejable); este comportamiento puede ser cambiado
(para openmath) desde los menús desplegables de xmaxima (
Options->Plot
Windows).
- geomview
Otro programa de dibujo sólo para
plot3d en GnuLinux-Unix
parecido al formato openmath. El gráfico es
guardado en un fichero de nombre maxout.geomview para que sea leído
por geomview si está instalado en el sistema.
Si el gráfico va a ser guardado para su posterior utilización,
el formato [plot_format,gnuplot] es mi preferido, porque usando simultáneamente la opción [plot_terminal,tikz], genera un fichero en formato texto plano que resulta idóneo para gestionarlo en LaTeX (ver detalles).
- /* Con carácter global, salvo modificaciones posteriores */
set_plot_option([plot_format, openmath]);
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2]);
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],[plot_format,gnuplot]);
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],[plot_format, geomview]);
- [title, "Título"]
Establece el "Título" común de la imagen (con independencia del número de gráficos).
- [legend, "Leyenda1","Leyenda2"... ]
La leyenda de los gráficos generados con plot2d y plot3d
es contruida por Maxima usando cuando es posible la fórmula de la función
matemática que sirvió para generarlo. Esta opción permite cambiar tales
leyendas.
[legend, false... ]
Elimina las leyendas.
-
[xlabel, "Etiqueta"] [ylabel, "Etiqueta"]
[zlabel, "Etiqueta"]
Fija la "Etiqueta"
para cada eje. Si no se hace uso de la opción, mostrará el nombre de la
variable independiente en plot2d e implit_plot o de la
primera variable independiente en plot3d; en el caso de curvas
paramétricas corresponde a la primera expresión y lo mismo ocurre con las curvas
de nivel.
- plot2d([sin(x),cos(x)],[x,0,%pi],
[title, "Dos funciones importantes"]);
- plot2d([sin(x),cos(x)],[x,0,%pi],
[title, "Dos funciones importantes"],
[legend, "seno", "coseno"])$
- plot2d([sin(x),cos(x)],[x,0,%pi],
[legend, false], [title, "Gráficas de las funciones seno y coseno"],
[xlabel, "Eje OX"],[ylabel,"Eje OY"])$
- [x, Valor inicial, Valor final ] [y, Valor inicial, Valor final ] [z, Valor inicial, Valor final ]
Fija el intervalo a dibujar en los diferentes ejes, de forma independiente del dominio que tengan lasa variables en la definició de las funciones.
- [box,Valor]
Los valores admitidos son
true (opción por defecto) y false que elimina los ejes y la caja del
gráfico. Pero plot3d y plot2d tienen comportamientos diferentes.
- plot2d([sin(x),cos(x)],[x,0,4],
[x,-1,5], [y,-1.5,1.5],
[legend, false], [title, "Gráficas de las funciones seno y coseno"])$
- plot3d(x^2+y^2, [x, -1,1], [y, -1,1],
[box, false], [legend,false] )$
- / Con plot2d el comportamiento es distinto */
plot2d(log(x), [x, 1, 5],
[box, false], [legend,false] )$
- / Eliminar las marcas de escala en los ejes */
plot2d(log(x), [x, 1, 5],
[gnuplot_preamble, "unset xtics; unset ytics"] )$
- [nticks, Número ]
El entero positivo
Número determina la cantidad de puntos usados en la rutina de dibujo.
Cuando una curva regular aparece dibujada como poligonal, puede conseguirse el
efecto óptico adecuado utilizando esta opción. El valor por defecto es 10.
- [grid, Número 1, Número 2 ]
Es el análogo, en gráficos 3D,
a nticks y controla el número de puntos usado para dibujar la
figura. El valor por defecto es 30,30.
- [same_xy], [same_xyz]
Opciones para 2D y 3D, respectivamente, que utilizan la misma escala en los diferentes ejes. También puede usarse en la forma [same_xy, true] o el correspondiente false que es la opción por defecto.
- [style,Lista 1,Lista
2,...]
En los gráficos simples (o múltiples) dibujados con
plot2d determina la apariencia del trazo: color, líneas o puntos,
grosor... para cada uno de los gráficos (1,2,...) de forma independiente.
Lista 1, Lista 2... son listas en el sentido Maxima y por
tanto delimitadas por corchetes. El primero de los elementos de tales listas es
una palabra clave elegida entre las siguientes:
lines para dibujar
líneas,
points para dibujar puntos aislados,
linespoints para
segmentos y puntos y
dots para pequeños puntos aislados;
en el caso
particular de gnuplot existe además impulses
Los siguientes
elementos de la lista son uno o más números, separados entre sí y de la palabra
clave por comas, que sirven para determinar el color, grosor, etc. Los detalles
aparecen a continuación.
El parámetro lines acepta uno o dos
números (separados de lines y entre sí por comas); el primero fija el grosor de
la línea (sin unidad) y el segundo el color de acuerdo con las correspondencias
1 azul,
2 rojo,
3 magenta,
4 naranja,
5 marrón,
6 lima,
7 agua.
Esto se aplica
a la pantalla X11, pero puede cambiar con otro tipo de salidas.
El parámetro points acepta de uno a tres números enteros; el primero
corresponde al radio (grosor) del punto, el segundo selecciona el color, usando
el mismo código de correspondencia que lines y finalmente el tercero es
usado sólo por Gnuplot y permite sustituir los puntos por otros objetos. Los
objetos disponibles y sus códigos numéricos son:
1 círculos (defecto),
2 circunferencias,
3 signo +,
4 signo x,
5 signo *,
6 cuadrados rellenos,
7 cuadrados vacíos,
8 triángulos rellenos,
9 triángulos vacíos,
10 variante de triangulos rellenos,
11 variante de triángulos vacíos,
12 rombos rellenos,
13 rombos vacíos.
- [palette, Paleta]
Este parámetro controla la
apariencia de los gráficos 3D. Cuando no se usa los gráficos se dibujan usando
una gama de colores rellenos y cambiantes en la dirección del eje Z para marcar
las alturas de acuerdo con ciertos patrones definidos por defecto. Cuando en
Paletas aparece false los colores de relleno desaparecen y
únicamente se muestra una "malla" de curvas, usando un único color para cada
superficie (o dos para diferenciar las caras). El visualizador
openmath va haciendo un uso cíclico de dichos patrones para
identificar las superficies visualmente mediante la paleta correspondiente,
mientras que gnuplot y geomviev utilizan una única
paleta.
Cada paleta es una lista con una palabra seguida de cuatro números.
Las palabras corresponden al atributo que se está parametrizando y son: hue,
saturation, value.
Los tres primeros números son decimales entre 0 y 1,
definen las características de un color básico que se asigna al mínimo valor de
z. Las palabras especifican cual de los tres atributos (hue, saturation or
value) se incrementará de acuerdo con los valores de z.
El cuarto número indica
el incremento correspondiente al máximo valor de z. Este cuarto número puede ser
mayor que 1 o negativo.
Algunos ejemplos del uso de
palette
- plot3d(x^2+2*y^2,[x,-1,1],[y,-1,1])$
- plot3d(x^2+2*y^2,[x,-1,1],[y,-1,1],
[palette,false])$
- plot3d(x^2+2*y^2,[x,-1,1],[y,-1,1],
[palette,[hue, 0.95, 0.7, 0.8, 0.5]])$
- plot3d(x^2+2*y^2,[x,-1,1],[y,-1,1],
[palette,[value, 0.95, 0.7, 0.8, 0.5]])$
- color[color, color_1, ..., color_n]
Cuando se
dibujan varios gráficos con el comando pot2d cada uno de ellos
tiene un color diferente de acuerdo con la secuencia siguiente: azul, rojo,
verde, magenta, negro y cian. En caso de que hayan más de seis gráficos se
repite cíclicamente la secuencia. Lo mismo se aplica al comando
implicit_plot. En el comando plot3d con la opción
[palette,false] ocurre lo mismo. La opción color
permite modificar la lista de los colores establecidos por defecto.
Los
colores permitidos en gnuplot son los que antes hemos mencionado, en caso de
poner otro se sustituye automáticamente por el negro. En cambio openmath permite
toda la gama de colores que se identifican en formato RGB de la forma
"#RRGGBB" correspondiente a la notación hexadecimal
- plot2d([sin(x)/2,cos(x)],[x,-%pi,%pi],
[color,black,green])$
- plot2d([sin(x),cos(x)],[x,-%pi,%pi],
[color,black,green], [plot_format,openmath] )$
- plot2d([(sin(x))/2,cos(x)],[x,-%pi,%pi],
[color,black,green],
[gnuplot_preamble,"set key top left"] /* véase Opciones específicas para Gnuplot */
)$
- plot2d([(sin(x))/2,cos(x)],[x,-%pi,%pi],
[gnuplot_preamble,"set key bottom"] /* véase Opciones específicas para Gnuplot */
)$
- plot3d(x^2+2*y^2,[x,-1,1],[y,-1,1],
[palette,false],
[color,black] )$
- plot3d(x^2+2*y^2,[x,-1,1],[y,-1,1],
[palette,false],
[box,false],
[color,"#088A4B"],
[plot_format,openmath])$
- [elevation, Número] y [azimuth,
Número]
Son dos parámetros que permiten cambiar el "punto de mira" del
gráfico 3D (en vertical y horizontal, respectivamente). Tienen como valores por
defecto 60 y 30; aparecen indicados cuando se visualiza el gráfico con las
plot_option: en gnuplot como un par de números y en
openmath con su propio nombre y números. Tales números van
cambiando al mover el gráfico con ayuda del ratón, lo que permite, encontrar de
forma interactiva, los valores más adecuados para los mismos en un gráfico 3D
concreto; esto resulta muy útil cuando se persigue generar un fichero definitivo
(digamos eps o pdf) para usarlo en otro lugar.
- plot3d(x^2-2*y^2,[x,-1,1],[y,-1,1]);
- plot3d(x^2-2*y^2,[x,-1,1],[y,-1,1],
[plot_format,xmaxima])$
- plot3d(x^2-2*y^2,[x,-1,1],[y,-1,1],
[elevation,70],
[azimuth,80]);
- [transform_xy, Transformación]
Esta opción
actualmente soporta, por defecto, dos valores para Transformación:
polar_to_xy que permite dibujar en coordenadas cilíndricas y
spherical_to_xyz que permite dibujar en coordenadas esféricas.
Pero en realidad el argumento Transformación puede ser cualquier cambio de
coordenadas creado con ayuda de la opción
[make_transform,
[Variables],fx,fy,fz] donde [Variables] es la lista con las
tres nuevas variables que harán el papel de las x,y,z y siendo fx,fy,fz las
funciones que expresan a las variables euclídeas x,y,z en términos de las nuevas
variables.
- /* Paraboloide de revolución en torno al eje Z */
plot3d(r^2,[r,0,1],[phi,0,2*%pi],
[transform_xy,polar_to_xy]);
- /* Creamos manualmente cilindricas con make_transform */
cilindricas : make_transform([r,phi,z],r*cos(phi),r*sin(phi),z )$
/* y ahora hacemos uso de cilindricas: más fácil de recordar */
plot3d(r^2,[r,0,1],[phi,0,2*%pi],
[transform_xy,cilindricas]);
- /* Superficie esférica de radio 2 */
plot3d(2,[theta,0,%pi],[phi,0,2*%pi],
[transform_xy,spherical_to_xyz],
[legend,false])$
- /* Creamos manualmente el comando esfericas con make_transform */
esfericas : make_transform([theta,phi,r],r*sin(theta)*cos(phi),r*sin(theta)*sin(phi),r*cos(theta) )$
/* y ahora hacemos uso de comando: más fácil de recordar */
plot3d(2,[theta,0,%pi],[phi,0,2*%pi],
[transform_xy,esfericas],
[legend,false])$
- [run_viewer, true]
Permite que los gráficos,
después de generar el correspondiente fichero gráfico, sean mostrados por el
visualizador que corresponda: gnuplot, mgnuplot, geomview o ps (en openmath la
opción, lógicamente, no tiene efecto). Para que funcione satisfactoriamente el
sistema debe estar adecuadamente configurado; en caso contrario la visualización
habrá de ser realizada manualmente con el visualizador oportuno. Cuando se
indica false, Maxima no hace llamadas a programas externos para
visualizar los gráficos: se limita a guardar el correspondiente
maxout.plot_format (donde la extensión plot_format coincide con uno de
los formatos ya explicados) que será reescrito con cada nuevo gráfico, por lo
que es necesario guardarlo previamente si se desea que esto no ocurra.
En el
caso de gnuplot profundizaremos posteriormente en este tema.
- [adapt_depth,
Número]
Parámetro técnico que determina el número de divisiones
realizadas en la rutina adaptativa de dibujo. El valor por defecto es 10
- [ps_file, "Nombre"] [pdf_file, "Nombre"] [svg_file, "Nombre"]
En lugar de mostrar la salida en
pantalla envía la salida directamente a un fichero en uno de los formatos indicados.
Realmente, tal cosa puede hacerse desde la propia ventana en que se visualiza el gráfico.

- plot3d(x^2+y^2, [x, -2, 2], [y, -2, 2],
[ps_file,"grafico1.ps"])$
- plot3d(x^2+y^2, [x, -2, 2], [y, -2, 2],
[pdf_file, "grafico1.pdf"],
[box, false],
[legend, false] )$
- [plot_realpart, false]
En la opción por defecto
false cuando se trata de dibujar una función compleja sólo aparecen
dibujados los puntos en los que la parte imaginaria es 0. Cuando se le asigna el
valor true aparece dibujada la parte real de la función aunque no sea
nula la parte imaginaria de la variable
- plot2d (log(x), [x, -5, 5],
[plot_realpart, false]);
- plot2d (log(x), [x, -5, 5],
[plot_realpart, true]);
 Opciones específicas para Gnuplot
Opciones específicas para Gnuplot
Gnuplot es un potente programa de dibujo con
multitud de posibilidades. Pero cuando Maxima realiza un dibujo utilizando
Gnuplot lo que hace es generar una lista ordenadas de puntos (a través de sus
coordenadas) que Gnuplot posiciona y enlaza entre sí, generalmente, mediante
segmentos (aunque esta cuestión puede ser controlada). Pero no todas
las posibilidades de Gnuplot están implementadas como comandos de Maxima. No obstante, Maxima implementa la opción gnuplot_preamble (más
abajo descrita) que permite añadir al preámbulo del fichero instrucciones
adicionales de acuerdo con la sintaxis de Gnuplot. Por supuesto, Gnuplot puede
realizar gráficos de forma totalmente independiente de Maxima.
Formatos en los que se pueden guardar los gráficos
El programa gnuplot es capaz de guardar el gráfico en una gran variedad de formatos que incluye los
habituales (postscript, png, jpeg) y otros menos habituales (latex, pstricks, tikz,
eepic, tpic, dxf, svg). La instrucción gnuplot para elegir cada uno de ellos es
"set terminal Nombre". Estos terminales de gnuplot (al menos parcialmente) pueden ser seleccionados
utilizando la siguiente opción:
- [gnuplot_term, Terminal ]
Actualmente Maxima permite los siguientes valores para esa elección de Terminal:
- default el gráfico aparece en una ventana independiente (es la opción por defecto)
- ps el gráfico es enviado a un fichero postscript de nombre
maxplot.ps
- pdf el gráfico es enviado a un fichero pdf de nombre
maxplot.pdf
- pstricks el gráfico es enviado a un fichero pstricks de nombre
maxplot.pstricks
- tikz el gráfico es enviado a un fichero tikz de nombre
maxplot.tikz
Este formato genera un archivo de texto plano idóneo para ser insertado
en LaTeX porque permite que los textos, las fórmulas, los colores... sean los mismos que aparecen
en el resto del texto LaTeX; además al ser editable se pueden hacer ajustes a posteriori por ejemplo para controlar grosores y tipos de las líneas, colores, reubicar textos...
El fichero maxplot.tikz se carga en LaTeX mediante \input{maxplot.tikz} pero requiere cargar en el preámbulo del fichero .tex el paquete gnuplot-lua-tikz.sty que está disponible junto con otro elemento en el archivo gnuplot-tikz.zip
- svg el gráfico es enviado a un fichero svg de nombre
maxplot.svg
- Los anteriores son los más aconsejables porque producen gráficos vectoriales de buena
calidad. Pero hay otros; entre ellos se encuentran:
latex (picture de LaTeX), pslatex
(picture+ps), eepic, jpeg, png, postscript,
tpic, dxf (autocad).
Veamos algunos ejemplos; en caso de generarse gráficos en formatos ps, pdf, svg, png... los correspondientes ficheros estarán en su carpeta de usuario, que en GNU/Linux corresponde a su home.
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[plot_format, gnuplot], [gnuplot_term,ps]);
Si la
BoundingBox no está ajustada a sus necesiades puede usar el programa ps2eps para conseguir un mejor ajuste
automatizado, o bien editar manualmente el fichero generado con un editor sólo
texto para personalizar la BoundingBox. Mediante el programa epstopdf puede
convertirse el gráfico a formato pdf si fuera necesario.
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[plot_format, gnuplot], [gnuplot_term, pdf]);
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[plot_format, gnuplot], [gnuplot_term, svg]);
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[plot_format, gnuplot], [gnuplot_term, tikz]);
- [gnuplot_out_file, "NombreFichero"]
Es un
complemento opcional muy útil para gnuplot_term ya que permite elegir el
"NombreFichero" de la salida en lugar del nombre estándar que lo pone
maxplot.gnuplot_term, evitando así que se reescriba con cada utilización.
plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[plot_format, gnuplot], [gnuplot_term,jpeg],
[gnuplot_out_file, "Figura.jpg"]);
Pasando parámetros a Gnuplot de forma directa
El parámetro gnuplot_preamble es de utilidad cuando los demás
opciones resultan insuficientes. La idea es añadir, en la cabecera del documento que Maxima genera, código adicional destinado a Gnuplot.
- [gnuplot_preamble,
"opcion_1;opcion_2;...opcion_n"]
Permite introducir en el preámbulo del fichero gráfico los
comandos de Gnuplot que no están directamente disponibles a través del lenguaje
de Maxima. Pero el uso de esta opción requiere conocer con detalle el lenguaje de Gnuplot, que es
más rico que el que actualmente se puede utilizar desde las opciones de Maxima contempladas en plot2d y plot3d.
Los comandos draw2d y draw3d del paquete draw incorporan más posibilidades a este respecto y recomendamos su utilización.
Evidentemente para poder sacarle partido a gnuplot_preamble es necesario conocer los valores
admisibles, es decir, las posibilidades de Gnuplot y su sintaxis. Esto excede
los objetivos de este Manualico. Encontrará referencias al final de esta página.
A continuación se muestran algunos de los valores que he usado. Como las opciones de esta sección están destinadas a Gnuplot, conviene recordar que puede ser necesario comunicárselo explícitamente a Maxima mediante [plot_format, gnuplot]
- set title 'Título del gráfico'
Pone el 'Título del gráfico'
- plot2d([sin(x),x, x-x^3/6 ],[x,-2,2],
[legend, "sin(x)","Taylor1","Taylor3"],
[gnuplot_preamble,"set title 'El seno y sus desarrollos de Taylor de orden 1 y 3'"] )$
El ejemplo precedente es irrelevante, en el sentido de que el resultado puede ser generado reemplazando la última línea
por [title, "El seno y sus desarrollos de Taylor de orden 1 y 3"], pero sirve como ilustración sencilla del uso de gnuplot_preamble
- set key Posición
Fija la Posición de la leyenda de los elementos
gráficos. Por defecto están situados arriba a la derecha. Valores básicos son
left, right, top, bottom, outside,
bellow (pudiendo utilizarse más de uno).
unset key eliminas tales leyendas
- plot2d([sin(x),x, x-x^3/6 ],[x,-2,2],
[legend, "sin(x)","T1","T3"],
[gnuplot_preamble,"set key left top;set title 'El seno y sus desarrollos de Taylor de orden 1 y 3'"])$
- set label
Permite poner etiquetas en posiciones arbitrarias
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[xlabel, "Eje X"],
[gnuplot_preamble,"set label 'Punto de silla' at 0,0,-6 rotate by 90 textcolor lt 1"]);
- lista:[[0,0],[1.5,0.5],[1,1.5],[0,0]]$
plot2d( [[discrete,lista],[discrete,lista]],
[style,[lines,4,1],[points,2,2,1]],
[x,0,2],[y,0,2],
[ylabel,""],
[xlabel,""],
[gnuplot_preamble, "set label 'A' at -0.05,0.05; set label 'B' at 1.52,0.51; set label 'C' at 1,1.58; unset xtics; unset ytics; unset key "] )$
- f(x):= if x< 1 then -0.1 else x-1.1$ plot2d(f(x), [x,0,2],
[plot_format, gnuplot],
[y,-0.3,1.5],
[ylabel, "C: valor de la call"],
[xlabel, "S: cotización del subyacente"],
[style,[lines, 4,1]],
[title, "Diagrama payoff de una call option"],
[gnuplot_preamble, "unset key; set xtics (' ' 0 ,'K' 1); set label 'precio de ejercicio' at 1,0.1 rotate by 90;"]
)$
- set noautoscale
Por defecto Gnuplot autoescala todos los ejes para que
la gráfica quepa en la ventana; este parámetro evita tal comportamiento.
- plot2d(cos(x),[x,0,50],
[y,-1.5,1.5],
[gnuplot_preamble, "set noautoscale"])$
- set logscale (set nologscale)
Permite fijar escala logarítmica en uno
o varios ejes. Observe la diferencia en el ejemplo
- plot2d(log(x),[x,1,10])$
- plot2d(log(x),[x,1,10],
[gnuplot_preamble, "set logscale x"])$
- set xtics (set ytics)
Controla donde aparecen las
marcas en los ejes y, eventualmente, etiquetas no numéricas en posiciones
numéricas.
unset xtics suprime las marcas del eje X.
- plot2d(log(x),[x,1,10],
[gnuplot_preamble, "set xtics (1,2,9)"])$
- plot2d(sin(x),[x,0,7],
[gnuplot_preamble,"set xtics ('0' 0, 'pi' 3.1416, '2pi' 6.2832)"])$
- plot2d(log(x), [x, 1, 5],
[gnuplot_preamble, "unset xtics; unset ytics"] /* elimina las marcas en ambos ejes */
)$
- set view angulo 1,angulo 2,escala 1,escala 2
Cambia el punto de mira en gráficos tridimensionales
(los dos primeros) y la escala (los dos segundos).
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[gnuplot_preamble,"set view 30,240,1,1.4"])$
- set contour ??
Permite dibujar las curvas de nivel de acuerdo con lo indicado en ??. Valores posibles son: base; surface, o both, cuyo nombre es autoexplicativo para quien conoce el inglés.
- plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[gnuplot_preamble,"set contour both"]);
- unset colorbox
No dibuja la barra con la escala de altura.
- plot3d(sqrt(1-x^2-y^2),[x,-1,1],[y,-1,1],
[legend,false],
[gnuplot_pm3d,true],
[gnuplot_preamble,"unset xtics; unset ytics; unset colorbox"])$
- set polar (unset polar)
Permite interpretar la función como escrita en coordenadas polares o cartesianas en gráficos 2d
- plot2d( 3*cos (2*t), [t,0,2*%pi])$
- plot2d( 3*cos (2*t),[t,0,2*%pi],
[gnuplot_preamble, "set polar"])$
- set border Opciones
Permite poner diferentes tipos de borde
al gráfico
set noborder elimina los bordes
- plot2d( 3*cos (2*t),[t,0,2*%pi],
[gnuplot_preamble, "set border 1"] /* cambie 1 por otro número y experimente */
)$
- plot3d(x^2+y^2,[x,-1,1],[y,-1,1],
[gnuplot_preamble,"set border 4095"])$
- plot3d(x^2+y^2,[x,-1,1],[y,-1,1],
[gnuplot_preamble,"set border 127+256+512"])$
- set style
Fija el estilo por defecto para funciones, datos, líneas,
flechas, rellenos,... Tiene una enorme riqueza de posibilidades que no podemos
enumerar aquí. La opción style suele ser suficiente.
- set terminal y set output
Son otras opciones de Gnuplot que pueden ser utilizadas para conseguir exportar el gráfico a derminados formatos. Pero, como en el caso precedente, la utilización de las opciones para exportar gráficos suele ser suficiente.
- set xzeroaxis set yzeroaxis (set noxzeroaxis)
Dibuja los ejes de coordenadas en gráficos (pueden decirse las especificaciones de tipo de línea,
etc.)
- plot2d([sin(x),x, x-x^3/6 ],[x,-2,2],
[legend, "sin(x)","T1","T3"],
[gnuplot_preamble,
"set key left;set xzeroaxis linetype 5 linewidth 2.5; set yzeroaxis linetype 5 linewidth 2.5 "])$
Dynamics
Un punto fijo atractivo de una función F es un punto z tal que F(z)=z que además cumple que la sucesión x[1], F(x[1])=x[2],... F(x[n])=x[n+1]... converge a z.
El teorema del punto fijo de Banach se ocupa de precisar condiciones de existencia.
El paquete dynamics de Maxima (que puede ser necesario cargar previamente mediante el correspondiente comando load en versiones antiguas de Maxima) permite la visualización gráfica de la trayectoria de un punto a través de la iteración mediante una función F utilizando el comando
- staircase(F, ValorInicial, NúmeroTérminos, opciones);
que dibuja un diagrama de la sucesión con el NúmeroTérminos indicado a partir del ValorInicial en el dominio de la función F construido mediante la relación recurrente x[n]=F(x[n-1]).
Como ocurre con los gráficos generados con draw2d la variable opciones puede ser utilizada si se desea, y con la misma sintaxis descrita para aquel comando.
- staircase(cos(x), 1, 11, [x, 0, 1.2], [title, "Construcción recurrente de un punto fijo para la función coseno"])$
- staircase(x/(3-2*x), -1, 10, [y, -1.5, 0.5],[legend,"","y=x/(3-2*x)","y=x"])$
La sucesión recurrente definida por la función x/(3-2*x) y ValorInicial -1 es monótona creciente y acotada superiormente:
existe el límite de la sucesión y vale 0.
- staircase(x/(3-2*x), 1/4, 10, [legend,"","y=x/(3-2*x)","y=x"], [gnuplot_preamble,"set key top left"])$
La misma función, cuando el ValorInicial es 1/4 genera una sucesión monótona decreciente y acotada inferiormente: también existe el límite de la sucesión y vale 0.




 Ap_GraficaSucesionRecurrenteLimite.wxmx Ilustra la utilidad de
Ap_GraficaSucesionRecurrenteLimite.wxmx Ilustra la utilidad de staircase para visualizar convergencia de sucesiones recurrentes
Saber más






 Gráficos 2D con Maxima básico
Gráficos 2D con Maxima básico
 Gráficos 3D con Maxima básico
Gráficos 3D con Maxima básico



 Opciones
Opciones Opciones comunes
Opciones comunes
 Opciones específicas para Gnuplot
Opciones específicas para Gnuplot





