Integrales

  1. Integrales y primitivas
  2. Integración numérica

 

indice

Primitivas e integrales

Maxima es capaz de hacer primitivas e integrales para funciones de una variable. También puede realizar integrales utilizando métodos numéricos.

  1. integrate( x/(1+x^2), x );
  2. integrate( 1/(1+x^2), x, 0, 1 );
  3. integrate( 1/(1+x^2), x, 0, inf );
  4. integrate( 1/(1+x^3), x );
  5. integrate( sin(t*x), x );
  6. integrate( exp(-u^2), u, minf, inf );
  7. integrate( exp(-x^2), x);
  8. /* resultados en la consola */ 'integrate( exp(-x^2), x) = integrate( exp(-x^2), x); 'diff(erf(x),x)= diff(erf(x),x); 'integrate(exp(-u^2), u, minf, x) = integrate(exp(-u^2), u, minf, x);

La función erf, que ha aparecido en los ejemplos es conocida y utilizada por Maxima, se llama función de error de Gauss y aunque está demostrado que no puede ser escrita en términos de las funciones elementales (polinomios, fracciones, senos, cosenos...) es una función muy importante para la probabilidad y la estadística. Dibuje su gráfica con los comandos usando el comando draw2d o plot2d (véase la sección de gráficos)

Otro ejemplo de función cuya primitiva no puede ser expresada en términos de funciones elementales es sin(x)/x. Pero la primitiva existe para cualquier valor de x al ser una función continua. El único punto en el que la continuidad no es directa es para x=0.

limit( sin(x)/x, x, 0);

Pero el cálculo anterior despeja las dudas: definiendo la función en el punto x=0 como 1, la función sin(x)/x es continua. Pedimos a Maxima que calcule la primitiva, y el resultado lo expresa en términos de una nueva función que, como la precente, posiblemente sea desconocida para usted, pero no para Maxima. Las cuentas siguientes justifican la afirmación.

  1. integrate( sin(x)/x, x );
  2. diff( %, x );
  3. /* si lo piensa, es exactamente el integrando */ /* pero le pedimos a Maxima que reescriba el resultado */ trigrat(%);

En ocasiones, como ocurre en ejemplo que viene a continuación, que contiene parámetros, puede suceder que Maxima requiera información adicional sobre los mismos para poder calcular la integral.

  1. integrate(%e^(-a*x)*cos(b*x),x,0,inf);
  2. kill(all)$ assume(a>0)$ integrate(%e^(-a*x)*cos(b*x),x,0,inf);

Existe un paquete abs_integrate que permite calcular la integral definida de ciertos integrandos que contienen valores absolutos. Lo ilustramos a continuación con un ejemplo trivial, pero la cuestión no es tan simple como el ejemplo sugiere. El lector interesado debe buscar en el manual de Maxima las posibilidades y limitaciones del paquete.

  1. integrate(abs(x^3),x,-1,1);
  2. load(abs_integrate)$ integrate(abs(x^3),x,-1,1);

 

Cambio de variable: ayudando a Maxima

Empezamos con ejemplo sencillo

  1. 'integrate(sqrt(1-2*x^2),x);
  2. changevar('integrate(sqrt(1-2*x^2),x), sqrt(2)*x=sin(t),t,x);
  3. rootscontract(%); %,nouns; subst(t=asin(sqrt(2)*x),%);
  4. Maxima es capaz de calcular la primitiva de forma directa
    'integrate(sqrt(1-2*x^2),x) = integrate(sqrt(1-2*x^2),x);

Pero Maxima no siempre es capaz de calcular la primitiva por sí sólo.

f(x):= x*%e^asin (x)/sqrt(1-x^2);
integrate( f(x), x );

devuelve una primitiva simbólica a pesar de que, en este caso, puede obtenerse, mediante integración por partes, una primitiva expresable a través de funciones elementales haciendo el cambio de variable y=asin(x) .

Vamos a "guiar" a Maxima para que sea capaz de calcular la primitiva: un ejemplo interesante de mútua y fructífera colaboración.

  1. changevar(integrate( f(x), x ), y=asin(x),y, x );
    Maxima no simplifica, pero para un humano puede darse cuenta de que, una vez simplificado, se trata de una primitiva en la nueva variable que puede ser calculada y deshaciendo el cambio de variable se obtiene el resultado buscado.
  2. Vamos a hacerlo paso a paso (salidas en la consola)
    kill(all); f(x):= x*%e^asin (x)/sqrt(1-x^2); changevar(integrate( f(x), x ), y-asin(x),y, x ); rootscontract(%); I0 : trigsimp(%); assume( cos(y) > 0); fullratsimp(I0); assume( 0<y, y<%pi/2); I1 : fullratsimp(I0); I1,nouns; subst(y=asin(x),%);

 

El algoritmo de Risch

El algoritmo de Risch es un algoritmo utilizado para el cálculo de primitivas que transforma el problema original en un problema algebraico. Para usarlo en Maxima la sintaxis coincide con la del comando integrate

risch(función,variable)

  1. integrate(sqrt(9*x^4+4*x^2),x);
  2. risch(sqrt(9*x^4+4*x^2),x); /* Comprobamos el resultado derivando */ diff(%,x);

Ayudando a Maxima adecuadamente el comando integrate también puede obtener el mismo resultado

  1. print("primero reescribimos la raíz con ayuda de radcan")$ f:radcan(sqrt(9*x^4+4*x^2)); print("y ahora calculamos la primitiva")$ integrate(f,x);
  2. /* primero suponemos que x es positivo */
    assume(x>0);
    integrate(sqrt(9*x^4+4*x^2),x);
  3. /* olvidamos ahora la suposición y suponemos x negativo */ forget(x>0); assume(x<0); integrate(sqrt(9*x^4+4*x^2),x); print("Reflexione sobre los resultados")$

De hecho, para tratar de calcular una primitiva, Maxima realiza una batería de pruebas heurísticas y si con ninguna de ellas consigue su propósito, entonces emplea el algoritmo de Risch. Utilizando el comando risch tales pruebas heurísticas se evitan. Dos formas diferentes para conseguir el mismo efecto aparecen a continuación (la segunda es más fácil de recordar).

integrate(sqrt(9*x^4+4*x^2),x),risch;

La respuesta obtenida mediante un comando integrate puede contener, además de las funciones elementales, otras funciones especiales, entre ellas erf y beta

  1. integrate(x^2*exp(-x^2),x);
  2. assume(a>-1)$
    assume(b>-1)$
    integrate(x^a*(1-x)^b,x,0,1);

En http://en.wikipedia.org/wiki/Error_function puede encontrar más información sobre la función de error erf y la función beta http://en.wikipedia.org/wiki/Beta_function.

 

indice

Integración numérica

El cálculo de primitivas (integrales indefinidas) no siempre es posible y por ende hay ocasiones en que la imposibilidad de aplicar la fórmula de Barrow para calcular integrales definidas requiere la utilización de métodos numéricos para poder calcular de integrales.
Maxima implementa de forma nativa dos comandos con esa finalidad: romberg y quad_qags; tales comandos corresponden a métodos numéricos conocidos: el método de Romberg (véase http://en.wikipedia.org/wiki/Romberg%27s_method) y el método QUADPACK (http://en.wikipedia.org/wiki/QUADPACK).

Se trata de aproximaciones y los decimales coinciden sólo en las primeras cifras.

  1. plot2d(sin(exp(x^2)),[x,0,1]);
  2. integrate(sin(exp(x^2)),x,0,1);
  3. romberg(sin(exp(x^2)),x,0,1);
  4. quad_qags(sin(exp(x^2)),x,0,1);

Puede ser necesario prestar atención a las funciones e intervalos en que se aplica: para la función sin(x)/x el punto 0 resulta problemático para el comando romberg, aunque se trate de una función continua en dicho punto.

  1. /* la función es continua */
    plot2d(sin(x)/x,[x,-2,2]);
  2. romberg(sin(x)/x,x,0,1);
  3. /* el comando quad_qags no tiene problemas en el origen */ quad_qags(sin(x)/x,x,0,1);

Comparemos en el caso de la integral de Gauss

  1. integrate(exp(-x^2),x,0,inf);
    %,numer
  2. romberg(exp(-x^2),x,0,100);
  3. quad_qags(exp(-x^2),x,0,100);
  4. quad_qags(exp(-x^2),x,0,1000);

En el caso de romberg el valor 100 no puede incrementarse de forma significativa, lo cual no ocurre con quad_qags

indice

Algunas aplicaciones

áreas de figuras planas.
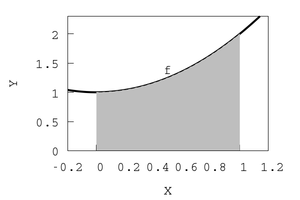
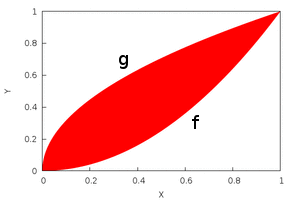
Para una función f(x)>0 integrable en [a,b] el valor de integrate(f(x),x,a,b) representa el "área bajo la curva" en el sentido que muestra el dibujo de la izquierda. Restando las correspondientes áreas (integrales) puede determinarse el área encerrada entre dos curvas g>f, que muestra la figura de la derecha.
Los códigos para crear los gráficos que aparecen más abajo forman parte de los ejemplos de la sección Gráficos con draw.


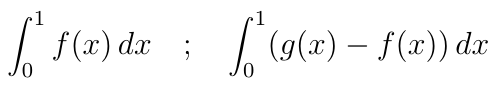
Volúmenes de sólidos de revolución.
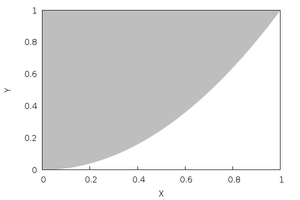
Rotaciones en torno al eje 0Y, o al eje 0X, de regiones planas delimitadas por una función f como las que las imágenes muestran, generan sólidos de revolución cuyo volumen puede ser calculado usando las fórmulas integrales que aparecen.



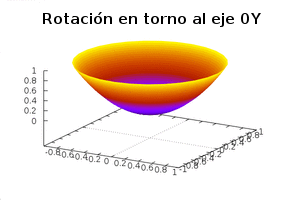
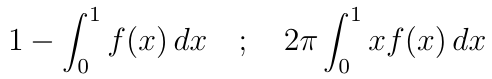
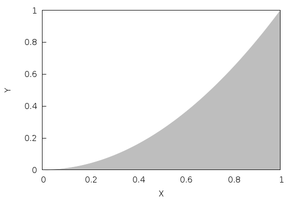
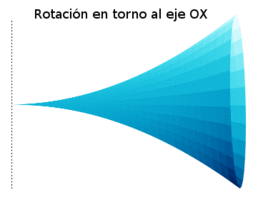
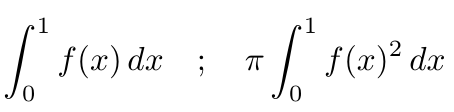
áreas de sólidos de revolución.
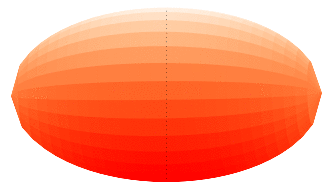
También pueden ser calculada el área de superficie de revolución obtenida girando la curva definida por una función f(x)>0 en torno al eje 0X.



 

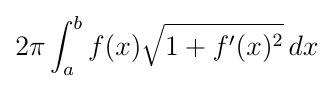
Integrales múltiples

El cálculo de integrales dobles (o triples) puede ser realizado, cuando el teorema de Fubini es aplicable, mediante integrales iteradas. Nos centraremos en el caso de integrales dobles para las que la intuición geométrica es más sencilla. Se trata de calcular integrales dobles

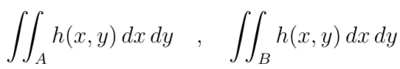
donde A y B son recintos planos similares a los que se muestran en las figuras siguientes, junto a las cuales se muestra el modelo de integral iterada a utilizar.




 

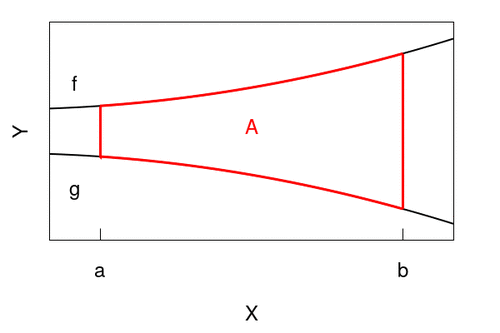
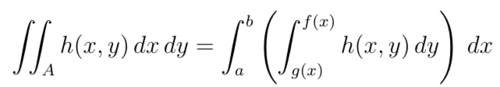
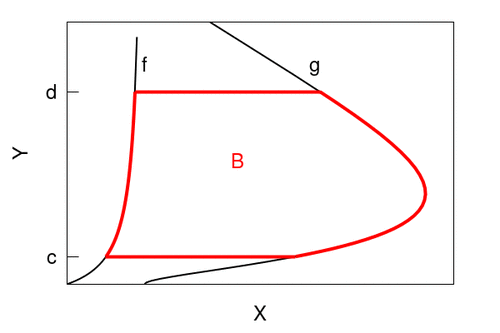
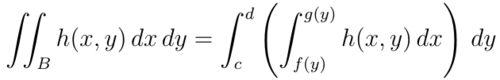
  1. Ap_Integrales.wxmx
  2. Ap_GenerarAnimaciones.wxmx Muestra visualmente la aproximación de las sumas de Riemann al área
  3. Ap_IntegralAreas.wxmx Ejemplos de cálculo de áreas
  4. Ap_IntegralVolumenes.wxmx Ejemplos de cálculo de volúmenes
  5. Ap_IntegralLongitudes.wxmx Ejemplos de cálculo de longitudes