TeX |
Cálculo y grafismo matemáticos en LaTeX usando Maxima y Gnuplot
Este apartado sólo resulta de interés para quienes necesiten escribir textos que incluyan cálculos o gráficos matemáticos y traten de conseguir que estos sean realizados automáticamente durante el proceso de compilación.
Maxima es un programa, con licencia GPL, capaz de realizar cálculo simbólico y numérico y de dibujar gráficos 2D y 3D. Permite, por ejemplo, calcular derivadas e integrales, hacer desarrollos de Taylor, calcular límites, realizar cálculo matricial, dibujar curvas y superficies, etc. Además es programable. La página principal es maxima.sourceforge.net y está implementado para Linux-Unix, MS-Windows y Mac OSX.
Los resultados obtenidos con Maxima, ya sean de naturaleza numérica o simbólica, pueden ser guardados en formatos susceptibles de ser incorporados a los documentos LaTeX. Pero ello requiere un trabajo de preparación de tales objetos y un mantenimiento de los mismos, previo a su incorporación en el documento LaTeX. El paquete «maxima» creado José Miguel Martín Planas hace posible integrar el documento LaTeX comandos de Maxima de suerte que el propio compilador TeX se encarga, cuando lee los comandos de Maxima existentes en el documento LaTeX, de guardar dichos comandos en un fichero auxiliar y realizar una llamada a Maxima para que interprete los comandos y produzca los resultados apetecidos para que en la próximas compilaciones del documento puedan ser utilizados los resultados proporcionados por Maxima. De este modo se consigue incluir en un único archivo LaTeX no sólo instrucciones para LaTeX sino también instrucciones para que Maxima realice cálculos que son necesarias para escribir el documento, lo cual simplifica enormemente el mantenimiento de documentos y comporta un ahorro de tiempo y esfuerzo. El paquete maxiplot, que utilizaremos aquí, es una adaptación del paquete de Martín Planas y permite incluir también código directo para Gnuplot.
![]() Con este vídeo en formato ogg podrá hacerse una idea de la forma en que Maxima trabaja para LaTeX.
Con este vídeo en formato ogg podrá hacerse una idea de la forma en que Maxima trabaja para LaTeX.
Instalación
Además del compilador LaTeX y del programa Maxima, necesitará:
- Un elemento destinado a LaTeX
- de nombre
maxiplot.sty, que debe ser colocado junto con los demás paquetes LaTeX, generalmente, en alguna carpeta dentro del directorio texmf/tex/latex (y posteriormente refrescar la base de datos de paquetes LaTeX instalados); si bien, este archivo puede ser colocado, como es habitual, en el directorio de trabajo. - Que los ejecutables de Maxima y Gnuplot estén en el path del sistema
- En el caso de Linux, una vez instalados, los ejecutables de Maxima y Gnuplot siempre están en el path. En el caso de MS-Windows hay que incluir en el path del sistema la carpeta correspondiente (por ejemplo c:\Archivos de programa/Maxima-5.18.1/bin) o bien crear un fichero maxima.bat para enlazar con el que existe en dicha carpeta y situarlo en alguna carpeta que ya estuviera en el path del sistema (por ejemplo en C:\Archivos de programa\Miktex2.7\miktex\bin). Algo similar hay que hacer para gnuplot.
Utilización del paquete
Lo primero es cargar en el preámbulo el paquete maxiplot
\usepackage{amsmath}
\usepackage[amsmath]{maxiplot}
El paquete contempla la opción amsmath cuyo uso recomendamos vivamente porque es necesaria cuando se usa el paquete amsmath que generalmente forma parte «obligada» de los preámbulos de los documentos LaTeX de matemáticas y por ello, aún siendo optativa, nuestra recomendación es incluir dicho parámetro.
El paquete maxiplot introduce unos pocos entornos y comandos específicos para la inclusión del código Maxima. Para la realización de cálculo nos interesan
\begin{maxima} Código Maxima \end{maxima} |
\imaxima{ Código Maxima } |
Y para la inclusión de gráficos desde Maxima con salida para Gnuplot nos interesan
\begin{maximacmd} Código Maxima \end{maximacmd} |
\imaximacmd{ Código Maxima } |
Si nuestro documento principal se llama NombreDocumento.tex, el contenido de estos entornos será guardado por el compilador TeX en el archivo NombreDocumento.mac para ser procesado después por Maxima. De modo que no podrá contener comentarios al estilo LaTeX (esto es, comenzando por %), puesto que este símbolo es utilizado por Maxima, aunque sí podrá contener comentarios al estilo Maxima, es decir de la forma /* comentario */. Las diferentes «unidades» del código Maxima deberán ir separadas entre sí por comas (,), debido a que serán tratados como variables de una función.
El entorno maxima y el comando \imaxima son esencialmente equivalentes, estando el comando pensado para incluirlo en escritura «en línea». Evidentemente para poder utilizar estos objetos es necesario conocer los comandos y la sintaxis de Maxima, al menos lo más básico.
El contenido del entorno maxima es escrito tal cual en el fichero .mac y posteriormente procesado por Maxima, pero los resultados producidos, en su caso, no se incorporan de forma directa en el documento; si se quieren incorporar hay que escribir el código LaTeX que corresponda de acuerdo con su naturaleza.
Para procesar el fichero .mac que el compilador TeX produce hay que utilizar Maxima, ya sea de forma manual o automática. La forma manual consiste en emplear (después de la compilación con TeX) la función bach de Maxima. Dicha función ejecuta un programa previamente guardado en un archivo, digamos NombreDocumento.mac, mediante la instrucción
maxima -b NombreDocumento.mac
En una segunda compilación los resultados producidos por Maxima serán incorporados a nuestro documento.
El proceso automático realiza las mismas operaciones que el manual, sólo que es el propio compilador TeX el encargado de ejecutar el batch con Maxima.
Para poder utilizar el procedimiento automático es necesario que nuestro compilador TeX soporte la opción write18 (las últimas versiones de las distribuciones TeTeX, Tex-live y MikTeX la soportan) y que el programa Maxima esté en el path del sistema. La forma de declarar la opción write18 para el compilador TeX depende del sistema (ver los detalles).
Realmente sólo se requiere utilizar la opción write18 una única vez para que se creen los ficheros auxiliares necesarios para todos los entornos maxima que existan en el documento en ese momento, pudiendo en lo sucesivo compilar con LaTeX en la forma estándar. Obviamente si se introducen nuevos entornos de este tipo será necesario compilar de nuevo con LaTeX utilizando la opción write18 al menos una vez. Una opción interesante es dejar activada permanentemente la opción write18 mientras se esté trabajando con un documento que la requiera. La única contraindicación es que si compila un fichero «malicioso» le está permitiendo acceder al sistema.
Los errores que, en su caso, produjera la acción del ejecutable Maxima quedarán reflejados en NombreDocumento.mac.log y si algo no funciona como se espera es conveniente leer dicho fichero para tratar de comprender las causas del problema.
En la realización de gráficos con Maxima y Gnuplot (véase la sección 2), Maxima se encarga de hacer las cuentas y crear una tabla de coordenadas que le transfiere a Gnuplot para que materialice el gráfico. Pero Gnuplot es un potente programa de grafismo que tiene capacidad por sí mismo de realizar las cuentas y de dibujar gráficos 2D y 3D. Tiene su propia sintaxis que es diferente de la de Maxima. Pero si conoce dicha sintaxis puede hacerse uso del entorno gnuplot implementado en el paquete maxiplot para producir gráficos con Gnuplot.
\begin{gnuplot} Código Gnuplot \end{gnuplot} |
\ignuplot{ Código Gnuplot } |
Al igual que el código maxima se guarda en un archivo de nombre NombreDocumento.mac que puede ser procesado manual (o automáticamente) por el ejecutable de Maxima, el código de los entornos gnuplot se guarda en un fichero de nombre NombreDocumento.gnuplot que puede ser ejecutado por Gnuplot, de forma automática (usando la opción write18) o de forma manual mediante
gnuplot 'load NombreDocumento.gnuplot'
0. Probar que funciona la instalación
Es muy aconsejable probar la instalación a nivel de la consola, porque no es infrecuente hacer algo mal en el proceso anterior con el resultado de que las cosas no funcionan.
- Descargue en su computadora el fichero test.tex y guárdelo en alguna carpeta que controle donde está.
- Abra una consola y sitúese en dicha carpeta (si no sabe como hacer esto en su sistema, deberá pedir ayuda a algún amigo más versado).
- Si usa Linux teclee en la consola
latex --shell-escape test
y abra con su visor de dvi el fichero test.dvi que se habrá generado. Repita la operación otra vez. Verifique que su visor de dvi le muestra el resultado deseado: un texto con una lista de ítems y una fórmula. De no ser así deberá leer el ficherotest.mac.logpara recabar información sobre donde puede estar el problema. - Si usa MS-Windows teclee en la consola
latex --enable-write18 test
y abra con su visor de dvi el fichero test.dvi que se habrá generado. Repita la operación otra vez. Verifique que su visor de dvi le muestra el resultado deseado. De no ser así deberá leer el ficherotest.mac.logpara recabar información sobre donde puede estar el problema. - Caso de no obtener el resultado buscado ejecute desde la consola
maxima -b test.mac
y vuelva a repetir el proceso anterior (según sus sistema). Si algo falla preste atención a los mensajes. - Una vez que esté seguro que desde la consola todo funciona como debe, configure adecuadamente su entorno de trabajo con LaTeX (algunos ejemplos de configuración)
1. Ejemplos de cálculo con el entorno maxima
\[
\begin{maxima}
f:x/(x^3 - 3*x +2),
tex('integrate(f,x)),
print("="),
tex(integrate(f,x)),
print("+K")
\end{maxima}
\]
|
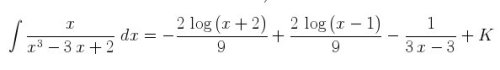
|
Si analizamos el código anterior observamos que se inicia con \[ y se finaliza con \] (entorno matemático centrado). El entorno maxima contiene código Maxima que pasamos a detallar.
f:x/(x^3 - 3*x +2)es una asignación o identificación de f con la expresión que aparecetex('integrate(f,x))significa que escriba en código tex, sin calcularla (lo cual se indica mediante la comilla') la integral indefinida de fprint("=")significa que imprima el signo =tex(integrate(f,x))significa que calcule el valor de la integral indefinida de f y escriba el resultado en código texprint("+K")significa que imprima +K
Como puede apreciarse la sintaxis es natural y relativamente simple conociendo los comandos de Maxima; pero hay que conocerlos. A continuación siguen otros ejemplos.
\[
\begin{maxima}
f:1/n^2,
numer:true,
tex('sum(f,n,1,100)),
print("="),
tex(nusum(f,n,1,100))
\end{maxima}
\]
|
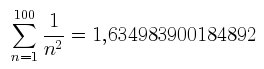
|
$$
\begin{maxima}
A:matrix([1,2,3],[4,8,5],[9,5,4]),
B:matrix([0,1,8],[1,7,0],[3,1,0]),
tex(A),
tex(B),
print("="),
tex(A.B)
\end{maxima}
$$
|
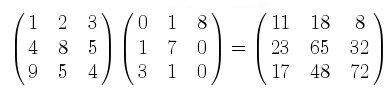
|
\[
\begin{maxima}
f:sin (x),
tex('f),
print("="),
tex(taylor(f,x,0,7)),
tex(o(x^7))
\end{maxima}
\]
|
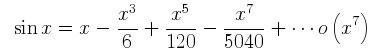
|
No debe pensarse que es necesario utilizar un entorno display de matemáticas. El ejemplo siguiente ilustra otro tipo de situación en el que las fórmulas van apareciendo después de realizar cálculos, de suerte que modificando sólo la primera línea en la que aparece definida la matriz se obtendría una colección diferente de fórmulas. También aparece utilizado el comando \imaxima además del entorno maxima.
La matriz
$\begin{maxima}
A:matrix([3,1],[2,4]),
tex('A),
print("="),
tex(A)
\end{maxima}$
tiene por adjunta
$
\begin{maxima}
print("\\mbox{Adj}(A)="),
tex(adjoint(A))
\end{maxima}
$
cuyo determinante es
$
\mbox{Det}(A)=
\imaxima{tex(determinant(A))}
$
y por consiguiente su inversa resulta ser
$$
\begin{maxima}
print("\\mbox{Inv}(A)="),
tex(invert(A))
\end{maxima}
$$
El polinomio característico de la matriz $A$ es
$
\mbox{Det}(A-xI)=
\begin{maxima}
P:expand(charpoly(A,x)),
tex(P)
\end{maxima}
$
cuyas raíces son
$\imaxima{tex(solve(P))}$
|

Observe la forma de escribir comandos tex dentro del código Maxima: \\hbox{Det} corresponde a \hbox{Det} y \\Longrightarrow correspondería a \Longrightarrow... |
2. Ejemplos de gráficos con el entorno maximacmd
Para la creación de un gráfico con Maxima se utiliza el entorno maximamcd y hay que indicar el nombre del gráfico que se creará, siendo ésta una responsabilidad del autor. Los ejemplos siguientes pueden servir como modelos para generar gráficos con Maxima e incluirlos en nuestro documento.
A diferencia de lo que ocurre con maxima e \imaxima, las unidades de Código Maxima van separados ahora por dólar ($) o punto y coma (;) puesto que son código nativo de Maxima.
Para experimentar, utilice un documento LaTeX cualquiera y vaya incluyendo en él algunos de los entornos que aparecen más abajo. Aquí se han incluido los ficheros gráficos generados en un entorno center, pero obviamente pueden ser incluidos en otros tipos de estructuras LaTeX.
Estos ejemplos gráficos son sólo un botón de muestra. Quizá suficiente para empezar. Pero para ir más lejos es necesario conocer la sintaxis de gnuplot (http://gnuplot.sourceforge.net) y Maxima. Una primera aproximación al tandem Maxima-gnuplot puede encontrarse en manualico (interactivo dentro de xMaxima) que hemos escrito.
Algunos de los ejemplos que siguen son utilizables por latex y pdflatex indistintamente, pero otros sólo lo son por uno de estos compiladores (lea cuidadosamente los comentarios de cada gráfico).
2.A) Gráficos eps «cerrados» válidos para latex y pdflatex
Los ejemplos que aparecen en este apartado pueden ser compilados indistintamente con latex+dvips o pdflatex, si bien en el segundo caso es necesario cargar el paquete epstopdf para permitir la conversión automática de gráficos eps a pdf mientras se
compila. Hemos denominado «cerrados» a estos gráficos debido a que utilizan un fichero eps no editable con facilidad, a diferencia de lo que ocurre en el apartado siguiente, donde los
gráficos («abiertos») son generados en formato sólo texto de acuerdo con cierta sintaxis que es interpretada durante la compilación.
En el caso de los gráficos abiertos (pictures y pspictures) puede modificarse a posteriori el código obtenido de forma manual, si así se desea. Esto, entre otras ventajas, hace posible que los textos en el gráfico, si los hay, utilicen los mismos tipos de letra que el texto ordinario, mejorando la estética.
1. Gráfico 2D
\begin{maximacmd}
plot2d([cos(x),sin(x^2)], [x,-3,3],
[plot_format, gnuplot],
[gnuplot_term, ps],
[run_viewer,false],
[gnuplot_out_file,"grafico1.eps"]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico1.eps}{\includegraphics[scale=0.60]{grafico1.eps}}{}
\end{center}
2. Gráfico 3D
\begin{maximacmd}
plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[plot_format, gnuplot],
[gnuplot_term, ps],
[run_viewer,false],
[gnuplot_out_file,"grafico2.eps"],
[gnuplot_pm3d, true]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico2.eps}{\includegraphics[scale=0.60]{grafico2.eps}}{}
\end{center}
2b. Gráfico 3D variante del anterior con algunas modificaciones: [gnuplot_pm3d, false], se quita el título de la superficie y se indican los ejes.
\begin{maximacmd}
plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[plot_format, gnuplot],
[gnuplot_term, ps],
[run_viewer,false],
[gnuplot_out_file,"grafico2b.eps"],
[gnuplot_curve_titles, "title ' ' "],
[gnuplot_preamble, "set xlabel 'X'; set ylabel 'Y'; set zlabel 'Z'"],
[gnuplot_pm3d, false]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico2b.eps}{\includegraphics[scale=0.60]{grafico2b.eps}}{}
\end{center}
3. Gráfico 2D en paramétricas
\begin{maximacmd}
plot2d( [parametric,2*sin(t),cos(t)], [t,0,2*%pi],[nticks,50],
[plot_format, gnuplot],
[gnuplot_term, ps],
[gnuplot_out_file,"grafico3.eps"],
[gnuplot_curve_titles, "title 'x^2/4+y^2=1'"]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico3.eps}{\includegraphics[scale=0.60]{grafico3.eps}}{}
\end{center}
4. Gráfico 2D en polares
\begin{maximacmd}
plot2d( 3*cos (2*t), [t,0,7],
[plot_format, gnuplot],
[gnuplot_term, ps],
[run_viewer,false],
[gnuplot_out_file,"grafico4.eps"],
[gnuplot_preamble, "set polar"]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico4.eps}{\includegraphics[scale=0.60]{grafico4.eps}}{}
\end{center}
5. Gráfico 3D en paramétricas
\begin{maximacmd}
plot3d( [cos(y)*(10.0+6*cos(x)), sin(y)*(10.0+6*cos(x)), -6*sin(x)], [x,0,2*%pi],[y,0,2*%pi],
[gnuplot_format, gnuplot],
[gnuplot_term, ps],
[run_viewer,false],
[gnuplot_curve_titles, "title 'El toro S^2'"],
[gnuplot_preamble,"set view 27, 50, 1, 1"],
[gnuplot_out_file,"grafico5.eps"]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico5.eps}{\includegraphics[scale=0.60]{grafico5.eps}}{}
\end{center}
Ejercicio: Marque y copie los códigos anteriores (uno a uno) e incorpórelos a un documento LaTeX que ya tenga escrito. Compile con latex y genere el fichero ps con dvips y compruebe el resultado. Haga lo mismo compilando con pdflatex para obtener una salida pdf.
Ejercicio: Si lo prefiere puede guardar y compilar este ejemplo con gráficos cerrados ya sea con latex o pdflatex (para incluir el último ejemplo que aparece comentado debe compilar con pdflatex). También encontrará aquí otro ejemplo con gráficos abiertos. Una vez guardado puede compilarlo con latex o pdflatex porque sólo usa código compatible. Hay apartados donde aparece código comentado y que puede ser descomentado selectivamente según el compilador que vaya a usar (puede ser necesario descargarse este archivo.
2.B) Gráficos «abiertos» (picture y pspicture) para latex y pdflatex
Ya hemos señalado a propósito de los gráficos cerrados las ventajas que pueden tener estos gráficos «abiertos». Con la aparición de los entornos tikzpicture su interés es menor del que antaño tenían. Además la puesta a punto del sistema LaTeX para la compilación con pdflatex de los gráficos que utilizan pspictures puede resultar complicada.
1. Gráfico 2D en polares que genera un entorno picture utilizable de forma directa por latex y pdflatex. Se consigue así un resultado mejor
integrado en el documento LaTeX, en cuanto a los textos, que los que se obtienen con los gráficos cerrados del apartado anterior (observe la forma en que se escribe el código LaTeX del
título de la gráfica). Las líneas curvas son menos eficientes que en otro tipo de salidas debido a la excasez de objetos disponibles en el entorno picture.
\begin{maximacmd}
plot2d( 3*cos (2*t), [t,0,7],
[plot_format, gnuplot],
[run_viewer,true],
[gnuplot_curve_titles, "title '$3\\cos 2t$'"],
[gnuplot_preamble,
"set terminal latex; set polar;
set output 'grafico6.pic'"]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico6.pic}{\input{grafico6.pic}}{}
\end{center}
3. Gráfico 2D que requiere el paquete pstricks (\usepackage{pstricks}) y, posiblemente, personalizar la salida grafico7.pst
Tal y como está aquí sólo puede ser compiladado con latex+dvips, pero siguiendo el modelo del ejemplo siguiente podría ser también utilizable por
pdflatex con ayuda de ps4pdf.
\begin{maximacmd}
plot2d(x*sin(x),[x,-2*%pi,2*%pi],
[plot_format, gnuplot],
[run_viewer,true],
[gnuplot_preamble,
"set terminal pstricks; set output 'grafico7.pst'"]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico7.pst}{\input{grafico7.pst}}{}
\end{center}
4. Gráfico 2D que requiere el paquete pstricks. A pesar de que el formato pstricks no es utilizable por pdflatex es posible con ayuda del paquete ps4pdf y ciertos ejecutables
configurar el sistema para que los formatos pstricks y eps sean utilizables por pdflatex. El truco está en automatizar lo que se haría a mano: compilar los gráficos con latex+dvips,
luego convertir los gráficos a formato pdf usando epstopdf y, finalmente, compilar de nuevo con pdflatex. Hemos realizado la configuración de nuestro sistema Linux para poder obtener de
forma automatizada una salida pdf (para más detalles véase ps4pdf)
\begin{maximacmd}
plot2d(x*sin(x),[x,-2*%pi,2*%pi],
[plot_format, gnuplot],
[run_viewer,true],
[gnuplot_preamble,
"set terminal pstricks; set output 'grafico8.pst'"]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico8.pst}{ \PSforPDF{\input{grafico8.pst}}}{}
\end{center}
2.C) Gráficos png para pdflatex
1. Gráfico 3D (png) El formato eps no es utilizable por pdflatex. En cambio si lo es el formato png, que además soporta transparencia. También puede usarse como salida para compilar con pdflatex.
\begin{maximacmd}
plot3d(-x^2+y^2,[x,-2,2],[y,-2,2],
[plot_format, gnuplot],
[run_viewer,true],
[gnuplot_preamble,"set terminal png; set output 'grafico9.png' "],
[gnuplot_pm3d, true]);
\end{maximacmd}
\begin{center}
\IfFileExists{grafico9.png}{\includegraphics[scale=0.60]{grafico9.png}}{}
\end{center}
3. Ejemplos de gráficos con el entorno gnuplot
Un ejemplo 3D
\begin{gnuplot}
set term postscript color solid
set output "toros.eps"
set parametric
set urange [0:2*pi]
set vrange [-pi:pi]
set isosamples 36,24
set hidden3d
set view 75,15,1,1
unset key
set ticslevel 0
x1(u,v)=cos(u)+.5*cos(u)*cos(v)
y1(u,v)=sin(u)+.5*sin(u)*cos(v)
z1(u,v)=.5*sin(v)
x2(u,v)=1+cos(u)+.5*cos(u)*cos(v)
y2(u,v)=.5*sin(v)
z2(u,v)=sin(u)+.5*sin(u)*cos(v)
set multiplot
splot x1(u,v), y1(u,v), z1(u,v) w pm3d, x2(u,v), y2(u,v), z2(u,v) w pm3d
splot x1(u,v), y1(u,v), z1(u,v) lt 3, x2(u,v), y2(u,v), z2(u,v) lt 5
\end{gnuplot}
\begin{center}
\IfFileExists{toros.eps}{\includegraphics{toros.eps}}{}
\end{center}
Un ejemplo 2D con relleno
\begin{gnuplot}
set output "normal.eps"
set term postscript portrait enhanced
set style fill solid 0.25
set size 1,0.5
set parametric
f(x)=exp(-x**2/2)*0.3989422
set xrange [-3:3]
set trange [-3:5]
unset xtics
set xlabel "Z" 8,0
path(t) = ( t<=1 ? f(t) : 0 )
fold(t) = (t <=1 ? t : 2 - t)
plot fold(t),path(t) notitle with filledcurves closed, t, f(t) notitle
\end{gnuplot}
\begin{center}
\IfFileExists{normal.eps}{\includegraphics{normal.eps}}{}
\end{center}
| GNU/Linux | LaTeX | Maxima | UMU |